为了加强食品安全管理,有关部门对某大型超市的甲、乙两种品牌食用油共抽取18瓶进行检测,检测结果分成“优秀”、“合格”、“不合格”三个等级,数据处理后制成以下折线统计图和扇形统计图.
⑴甲、乙两种品牌食用油各被抽取了多少瓶用于检测?
⑵在该超市购买一瓶乙品牌食用油,请估计能买到“优秀”等级的概率是多少?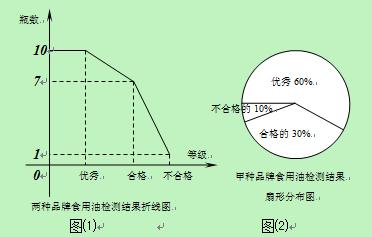
如图,已知D是BC的中点,过点D作BC的垂线交∠A的平分线于点E,EF⊥AB于点E,EG⊥AC于点G.求证:BF=CG.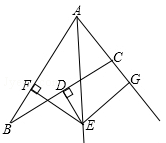
应用公式计算:
(1)1.02×0.98;
(2) ;
;
(3)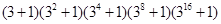 .
.
如图所示,在△ABC中,AB=AC,∠C=30°,AB⊥AD,AD=4cm,求BC的长.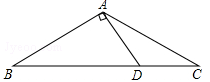
如图,△ABC中,∠A = 40°,∠B = 72°,CE平分∠ACB,CD⊥AB于D,DF⊥CE,求∠CDF度数.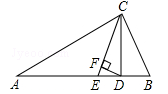
如图,在平面直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).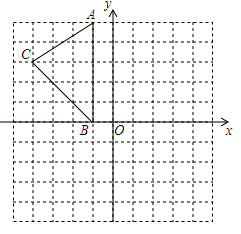
(1)在图中作出△ABC关于y轴的对称图形△A1B1C1;
(2)在y轴上找出一点P,使的PA+PB的值最小,直接画出点P的位置.