如图所示,过点F(0,1)的直线y=kx+b与抛物线 交于M(x1,y1)和N(x2,y2)两点(其中x1<0,x2<0).
交于M(x1,y1)和N(x2,y2)两点(其中x1<0,x2<0).
⑴求b的值.
⑵求x1•x2的值
⑶分别过M、N作直线l:y=-1的垂线,垂足分别是M1、N1,判断△M1FN1的形状,并证明你的结论.
⑷对于过点F的任意直线MN,是否存在一条定直线m,使m与以MN为直径的圆相切.如果有,请法度出这条直线m的解析式;如果没有,请说明理由.
某商场礼品柜台春节期间购进大量贺年卡,一种贺年卡平均每天可售出500张,每张盈利0.3元.为了尽快减少库存,商场决定采取适当的降价措施,调查发现,如果这种贺年卡的售价每降低0.1元,那么商场平均每天可多售出100张,商场要想平均每天盈利120元,每张贺年卡应降价多少元?
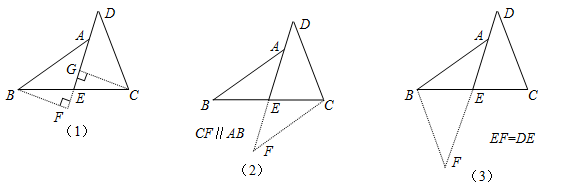
如图,点D,E在△ABC的边BC上,AB=AC,BD=CE.
求证:AD=AE.
选择适当方法解下列方程:
(1) ;(2)
;(2) ;
;
已知:如图,点C为线段AB上一点,△ACM、△CBN是等边三角形,可以说明:△ACN≌△MCB,从而得到结论:AN=BM.现要求: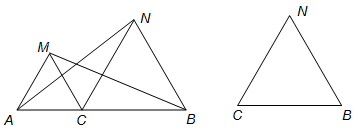
(1)将△ACM绕C点按逆时针方向旋转180°,使A点落在CB上.请对照原题图在下图中画出符合要求的图形(不写作法,保留作图痕迹).
(2)在(1)所得到的图形中,结论“AN=BM”是否还成立?若成立,请给予证明;若不成立,请说明理由.
(3)在(1)所得到的图形中,设MA的延长线与BN相交于D点,请你判断△ABD与四边形MDNC的形状,并说明你的结论的正确性.
(阅读下面的题目及分析过程,并按要求进行证明.
已知:如图,E是BC的中点,点A在DE上,且∠BAE=∠CDE.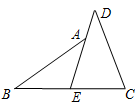
求证:AB=CD.
分析:证明两条线段相等,常用的一般方法是应用全等三角形或等腰三角形的判定和性质,观察本题中要证明的两条线段,它们不在同一个三角形中,且它们分别所在的两个三角形也不全等.因此,要证AB=CD,必须添加适当的辅助线,构造全等三角形或等腰三角形.
现给出如下三种添加辅助线的方法,请任意选择其中一种,对原题进行证明.