数学课堂上,徐老师出示一道试题:
如图(十)所示,在正三角形ABC中,M是BC边(不含端点B、C)上任意一点,P是BC延长线上一点,N是∠ACP的平分线上一点.若∠AMN=60°,求证:AM=MN.
(1)经过思考,小明展示了一种正确的证明过程.请你将证明过程补充完整.
证明:在AB上截取EA=MC,连结EM,得△AEM.
∵∠1=180°-∠AMB-∠AMN,∠2=180°-∠AMB-∠B,∠AMN=∠B=60°,∴∠1=∠2.
又CN平分∠ACP,∠4=∠ACP=60°.∴∠MCN=∠3+∠4=120°…………①
又∵BA=BC,EA=MC,∴BA-EA=BC-MC,即BE=BM.
∴△BEM为等边三角形.∴∠6=60°.
∴∠5=180°-∠6=120°.………②
∴由①②得∠MCN=∠5.
在△AEM和△MCN中,
∵
∴△AEM≌△MCN (ASA).∴AM=MN.
(2)若将试题中的“正三角形ABC”改为“正方形A1B1C1D1”(如图),N1是∠D1C1P1的平分线上一点,则当∠A1M1N1=90°时,结论A1M1=M1N1.是否还成立?(直接写出答案,不需要证明)
(3) 若将题中的“正三角形ABC”改为“正多边形AnBnCnDn…Xn”,请你猜想:当∠AnMnNn= °时,结论AnMn=MnNn仍然成立?(直接写出答案,不需要证明)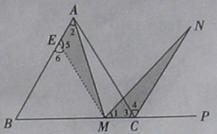
某出租公司有若干辆同一型号的货车对外出租,每辆货车的日租金实行淡季、旺季两种价格标准,旺季每辆货车的日租金比淡季上涨 .据统计,淡季该公司平均每天有10辆货车未出租,日租金总收入为1500元;旺季所有的货车每天能全部租出,日租金总收入为4000元.
(1)该出租公司这批对外出租的货车共有多少辆?淡季每辆货车的日租金多少元?
(2)经市场调查发现,在旺季如果每辆货车的日租金每上涨20元,每天租出去的货车就会减少1辆,不考虑其它因素,每辆货车的日租金上涨多少元时,该出租公司的日租金总收入最高?
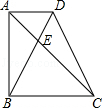
如图,在四边形 ABCD中, AD∥ BC, AB= BC,∠ BAD=90°, AC交 BD于点 E,∠ ABD=30°, AD= ,求线段 AC和 BE的长.
(注: )
某校为了解九年级学生的体育达标情况,随机抽取50名九年级学生进行体育达标项目测试,测试成绩如下表,请根据表中的信息,解答下列问题:
|
测试成绩(分) |
23 |
25 |
26 |
28 |
30 |
|
人数(人) |
4 |
18 |
15 |
8 |
5 |
(1)该校九年级有450名学生,估计体育测试成绩为25分的学生人数;
(2)该校体育老师要对本次抽测成绩为23分的甲、乙、丙、丁4名学生进行分组强化训练,要求两人一组,求甲和乙恰好分在同一组的概率.(用列表或树状图方法解答)
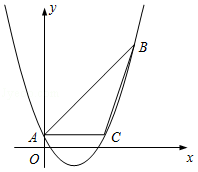
如图,已知抛物线 y= ax 2﹣2 x+ c经过△ ABC的三个顶点,其中点 A(0,1),点 B(9,10), AC∥ x轴.
(1)求这条抛物线的解析式;
(2)求tan∠ ABC的值;
(3)若点 D为抛物线的顶点,点 E是直线 AC上一点,当△ CDE与△ ABC相似时,求点 E的坐标.
某厂商投产一种新型科技产品,每件制造成本为18元,试销过程中发现,每月销售量 y(万件)与销售单价 x(元)之间的关系可以近似地看作一次函数 y=﹣2 x+100
(1)写出每月的利润 L(万元)与销售单价 x(元)之间的函数关系式;
(2)当销售单价为多少元时,厂商每月能获得312万元的利润?当销售单价为多少元时,厂商每月能获得最大利润?最大利润是多少?
(3)根据相关部门规定,这种科技产品的销售单价不能高于32元,如果厂商要获得每月不低于312万元的利润,那么制造出这种产品每月的最低制造成本需要多少万元?