一个口袋内装有大小相同的5 个球,其中3个白球分别记为A1、A2、A3;2个黑
球分别记为B1、B2,从中一次摸出2个球.
(Ⅰ)写出所有的基本事件;
(Ⅱ)求摸出2球均为白球的概率.
(本小题满分6分)
如图,在边长为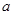 的菱形
的菱形 中,
中,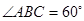 ,
,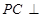 面
面 ,
, ,
, 、
、 分别是
分别是 和
和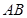 的中点.
的中点.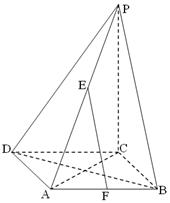
(1)求证: 面
面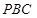 ;
;
(2)求证:平面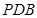 ⊥平面
⊥平面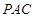 ;
;
(3)求 与平面
与平面 所成的角的正切值.
所成的角的正切值.
(本小题满分6分)
已知直线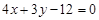 截圆心在点
截圆心在点 的圆
的圆 所得弦长为
所得弦长为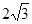 .
.
(1)求圆 的方程;
的方程;
(2)求过点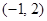 的圆
的圆 的切线方程.
的切线方程.
(本小题满分6分)
(1)计算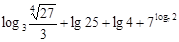
(2)已知 ,求
,求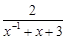 的值.
的值.
(本小题满分6分)
求经过两条直线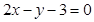 和
和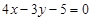 的交点,并且与直线
的交点,并且与直线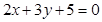 垂直的直线方程的一般式.
垂直的直线方程的一般式.
(本小题满分14分)
如图所示,在一个特定时段内,以点E为中心的10海里以内海域被设为警戒水域.点E正北40 海里处有一个雷达观测站A,某时刻测得一艘匀速直线行驶的船只位于点A北偏东30°且与点A相距100海里的位置B,经过2小时又测得该船已行驶到点A北偏东60°且与点A相距20
海里处有一个雷达观测站A,某时刻测得一艘匀速直线行驶的船只位于点A北偏东30°且与点A相距100海里的位置B,经过2小时又测得该船已行驶到点A北偏东60°且与点A相距20 海里的位置C.
海里的位置C.
(1)求该船的行驶速度(单位:海里/小时);
(2)若该船不改变航行方向继续行驶.判断它是否会进入警戒水域,并说明理由.