设△ABC的内角A,B,C的对边分别为a,b,c.已知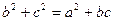 ,求:
,求:
(Ⅰ)A的大小;
(Ⅱ)若 ,求
,求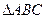 面积的最大值.
面积的最大值.
已知数列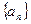 中,
中,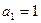 ,且
,且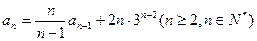 .
.
(1)求数列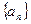 的通项公式
的通项公式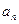 ;
;
(2)令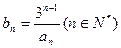 ,数列
,数列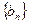 的前
的前 项和为
项和为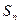 ,试比较
,试比较 与
与 的大小;
的大小;
(3)令 ,数列
,数列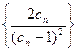 的前
的前 项和为
项和为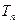 ,求证:对任意
,求证:对任意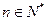 ,都有
,都有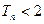 .
.
已知数列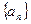 的前
的前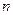 项和为
项和为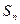 ,
,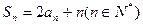 .
.
(1)求数列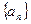 的通项公式
的通项公式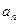 ;
;
(2)求数列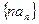 的前
的前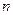 项和
项和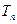 ;
;
(3)若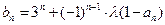 (
(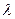 是非零常数),是否存在
是非零常数),是否存在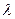 ,使得对任意
,使得对任意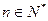 ,都有
,都有 若存在,求出
若存在,求出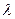 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
已知向量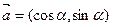 ,
, .
.
(1)若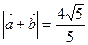 ,求
,求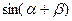 的值;
的值;
(2)若 且
且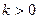 ,求
,求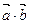 的最小值及此时向量
的最小值及此时向量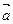 与
与 所成角的大小.
所成角的大小.
某单位建造一间背面靠墙的小房,地面面积为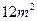 ,房屋正面每平方米的造价为
,房屋正面每平方米的造价为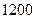 元,房屋侧面每平方米的造价为
元,房屋侧面每平方米的造价为 元,屋顶的造价为
元,屋顶的造价为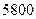 元.如果墙高为
元.如果墙高为 ,且不计房屋背面和地面的费用,问怎样设计房屋能使总造价最低?最低造价是多少?
,且不计房屋背面和地面的费用,问怎样设计房屋能使总造价最低?最低造价是多少?
已知向量 满足
满足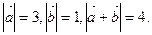
求(1)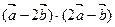 ;
;
(2)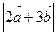 .
.