分解因式:
(1) m2+4m+4
(2) a2b-4ab2+3b3
(3)(x2+y2)2-4x2y2
如图,在平面直角坐标系中,点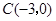 ,点
,点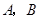 分别在
分别在 轴,
轴, 轴的正半轴上,且满足
轴的正半轴上,且满足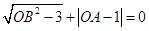 .
.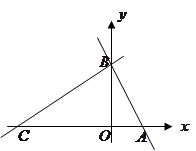
求点
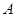 ,点
,点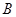 的坐标
的坐标若点
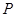 从
从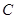 点出发,以每秒1个单位的速度沿线段
点出发,以每秒1个单位的速度沿线段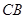 运动,连结
运动,连结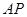 .设
.设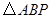 的面积为
的面积为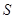 ,点
,点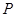 的运动时间为
的运动时间为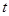 秒,求
秒,求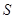 与
与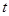 的函数关系式,并写出自变量的取值范围.
的函数关系式,并写出自变量的取值范围.在(2)的条件下,是否存在点
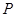 ,使以点
,使以点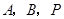 为顶点的三角形与
为顶点的三角形与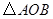 相似?若存在,请直接写出点
相似?若存在,请直接写出点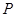 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
如图①,双曲线y=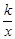 (k>0)与直线y=k'x交于A、B两点,点A在第一象限.
(k>0)与直线y=k'x交于A、B两点,点A在第一象限.若点A的坐标为(4,2),则点B的坐标为_______.若点A的横坐标为m,则点B的坐标可表示为_______.
如图②,过原点O作另一条直线l,交双曲线y=
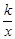 (k>0)于P、Q两点,点P在第一
(k>0)于P、Q两点,点P在第一
象限.①四边形APBQ的形状一定是
②设点A、P的横坐标分别为m、n,四边形APBQ可能是矩形吗?若可能,请直接写
出m、n应满足的条件;若不可能,请说明理由.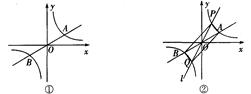
“五一”期间,为了满足广大人民的消费需求,某商店计划用160 000元购进一批家电,这批家电的进价和售价如下表:
若全部资金用来购买彩电和洗衣机共100台,则商家可以购买彩电和洗衣机各几台?
若在现有资金160 000元允许的范围内,购买上表中三类家电共100台,其中彩电台数和冰箱台数相同,且购买洗衣机的台数不超过购买彩电的台数,请你算一算,共有几种进货方案?哪种进货方案能使商店销售完这批家电后获得的利润最大?并求出最大利润.(利润=售价-进价)
如图,已知函数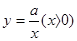 的图象与直线
的图象与直线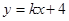 相交于点A(1,3)、B(
相交于点A(1,3)、B(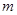 ,1)两点,
,1)两点,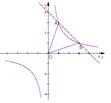
写出
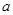 、
、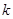 、
、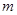 的值;
的值;求不等式
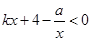 的解(请直接写出答案);
的解(请直接写出答案);求△AOB的面积。
某文具店老板第一次用1 000元购进一批文具,很快销售完毕,第二次购进时发现每件文具的进价比第一次上涨了2.5元,老板用2 500元购进了第二批文具,所购进文具的数量是第一次购进数量的2倍,同样很快销售完毕,两批文具的售价均为每件15元.第二次购进多少件文具?
文具店老板在这两笔生意中共盈利多少元?