为发展旅游经济．我市某景区对门票采用灵活的售票方法吸引游客．门票定价为50元/人．非节假日打4折售票．节假日按团队人数分段定价售票，即m人以下(含m人)的团队接原价售票；超过m人的团队．其中m人仍按原价售票．超过m人部分的游客打b折售票．设某旅游团人数为x人．非节假日购票款为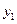
(元)，节假日购票款为
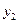(元)．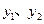
与x之间的函数图象如图8所示．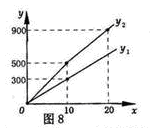
（1）观察图象可知：a=______；b=______；m=______；
（2）直接写出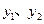与x之间的函数关系式：
（3）某旅行杜导游王娜于5月1日带A团．5月20日(非节假日)带B团都到该景区旅游．共付门票款1900元．A，B两个团队合计50人，求A，B两个团队各有多少人?
如图，双曲线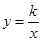
(x＞0)经过△OAB的顶点A和OB的中点C，AB∥x轴，点A的坐标为(2，3)．
(1)求k的值；
(2)若点D(3，m)在双曲线上，求直线AD的解析式；
(3)计算△OAB的面积．
已知A(x1，y1)，B(x2，y2)是反比例函数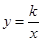
的图象上的两点，且x1－x2＝－2，x1·x2＝3，
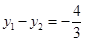，当－3＜x＜－1时，求y的取值范围．
[探究发现]如图①，已知△ABC是等边三角形，∠AEF＝60°，EF交等边三角形外角平分线于点F，当点E是BC的中点时，有AE＝EF成立．
[数学思考]某数学兴趣小组在探究AE与EF的关系时，运用“从特殊到一般”的数学思想，通过验证得出如下结论：
当点E是直线BC上(B，C除外)任意一点时(其他条件不变)，结论AE＝EF仍然成立．
假如你是该兴趣小组中的一员，请你从“点E是线段BC上的任意一点”；“点E是线段BC延长线上的任意一点”；“点E是线段BC反向延长线上的任意一点”三种情况中，任选一种情况，在图②中画出图形，并证明AE＝EF．
[拓展应用]当点E在线段BC的延长线上时，若CE＝BC，在图③中画出图形，并运用上述结论求出S△ABC︰S△AEF的值．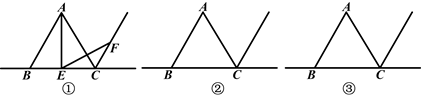
盐城电视塔是某市标志性建筑之一．如图，在一次数学课外实践活动中，老师要求测电视塔的高度AB．小明在D处用1m高的测角仪CD，测得电视塔顶端A的仰角为30°，然后向电视塔方向水平前进224m到达E处，又测得电视塔顶端A的仰角为60°，求电视塔的高度AB．(取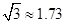
，结果精确到1m)
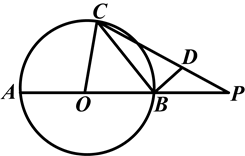
如图，AB是⊙O的直径，延长AB至P，使BP＝OB，BD垂直于弦BC，垂足为点B，点D在PC上．设∠PCB＝∠α，∠POC＝∠β，求证：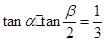
．