如图,互相垂 直的两条公路
直的两条公路 、
、 旁有一矩形花园
旁有一矩形花园 ,现欲将其扩建成一个
,现欲将其扩建成一个 更大的三角形花园
更大的三角形花园 ,要求
,要求 在射线
在射线 上,
上, 在射线
在射线 上,且
上,且 过点
过点 ,其中
,其中 米,
米,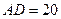 米. 记三角形花园
米. 记三角形花园 的面积为
的面积为 .
.
(1)设

 米,将
米,将 表示成
表示成 的函数.
的函数.
(2) 当
当 的长度是多少时,
的长度是多少时, 最小?并求
最小?并求 的最小值.
的最小值.
(3)要使 不小于
不小于 平方米,则
平方米,则 的长应在什么范围内?
的长应在什么范围内?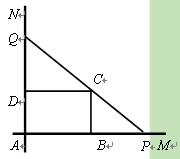
)某企业去年的纯利润为500万元,因设备老化等原因,企业的生产能力将逐年下降.若不能进行技术改造,预测从今年起每年比上一年纯利润减少20万元,今年初该企业一次性投入资金600万元进行技术改造,预测在未扣除技术改造资金的情况下,第n年(今年为第一年) 的利润为500(1+
的利润为500(1+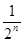 )万元(n为正
)万元(n为正 整数).
整数).
( Ⅰ)设从今年起的前n年,若该企业不进行技术改造的累计纯利润为
Ⅰ)设从今年起的前n年,若该企业不进行技术改造的累计纯利润为 万元,进行技术改造后的累计纯利润为
万元,进行技术改造后的累计纯利润为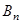 万元(须扣除技术改造资金),求
万元(须扣除技术改造资金),求 、
、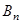 的表达式;
的表达式;
(Ⅱ)依上述预测,从今年起该企业至少经过多少年,进行技术改造后的累计纯利润超过不进行技术改造的累计纯利润?
( 12分)四边形ABCD,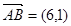 ,
,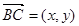 ,
,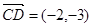 ,
,
(1)若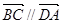 ,试求
,试求 与
与 满足的关系式
满足的关系式
(2)在满足(1)的同时,若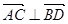 ,求
,求 与
与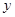 的值以及四边形ABCD的面积
的值以及四边形ABCD的面积
( 12分)已知: ,
,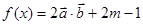 (
(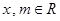 ).
).
(Ⅰ) 求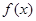 关于
关于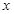 的表达式,并求
的表达式,并求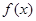 的最小正周期;
的最小正周期;
(Ⅱ) 若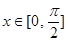 时,
时,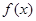 的最小值为5,求
的最小值为5,求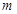 的值.
的值.
( 12分)已知等差数列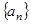 ,
,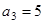 ,
,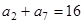
(1)求数列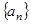 的通项公式
的通项公式
(2)设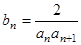 ,求数列
,求数列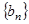 的前
的前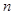 项和
项和
函数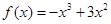 ,设
,设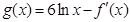 (其中
(其中 为
为 的导函数),若曲线
的导函数),若曲线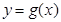 在不同两点
在不同两点 、
、 处的切线互相平行,且
处的切线互相平行,且 恒成立,求实数
恒成立,求实数 的最大值
的最大值