直线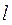 与抛物线
与抛物线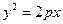 (p
(p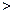 0)交于A、B
0)交于A、B 两点,且
两点,且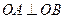 (O为坐标原点),求证:
(O为坐标原点),求证:
(1)A、B两点的横坐标之积,纵坐标之积都是常数;
(2)直线AB经过x轴上一个定点.
已知 ABC中,角A,B,C的对边分别为a,b,c, 若向量
ABC中,角A,B,C的对边分别为a,b,c, 若向量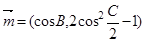 与向量
与向量 共线.
共线.
(1)求角C的大小;
(2)若 ,求a,b的值.
,求a,b的值.
已知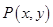 为函数
为函数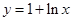 图象上一点,O为坐标原点,记直线
图象上一点,O为坐标原点,记直线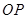 的斜率
的斜率 .
.
(Ⅰ)若函数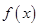 在区间
在区间
 上存在极值,求实数m的取值范围;
上存在极值,求实数m的取值范围;
(Ⅱ)设 ,若对任意
,若对任意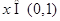 恒有
恒有 ,求实数
,求实数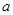 的取值范围.
的取值范围.
在平面直角坐标系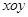 中,已知
中,已知 分别是椭圆
分别是椭圆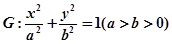 的左、右焦点,椭圆
的左、右焦点,椭圆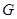 与抛物线
与抛物线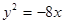 有一个公共的焦点,且过点
有一个公共的焦点,且过点 .
.
(Ⅰ)求椭圆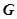 的方程;
的方程;
(Ⅱ)设直线 与椭圆
与椭圆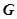 相交于
相交于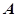 、
、 两点,若
两点,若 (
(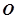 为坐标原点),试判断直线
为坐标原点),试判断直线 与圆
与圆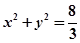 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.
如图,在底面为平行四边形的四棱柱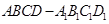 中,
中,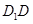
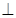 底面
底面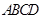 ,
,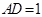 ,
,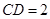 ,
,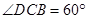 .
.
(Ⅰ)求证:平面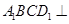 平面
平面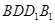 ;
;
(Ⅱ)若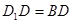 ,求四棱锥
,求四棱锥 的体积.
的体积.
设各项均为正数的数列 的前
的前 项和为
项和为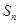 ,满足
,满足 且
且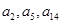 恰好是等比数列
恰好是等比数列 的前三项.
的前三项.
(Ⅰ)求数列 、
、 的通项公式;
的通项公式;
(Ⅱ)记数列 的前
的前 项和为
项和为 ,若对任意的
,若对任意的 ,
,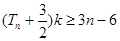 恒成立,求实数
恒成立,求实数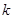 的取值范围.
的取值范围.