(本小题满分14分)
设数列{an}的前n项和为Sn,已知a1=1,且an+2SnSn-1=0(n≥2),
(1)求数列{Sn}的通项公式;
(2)设Sn=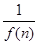 ,bn=f(
,bn=f(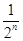 )+1.记Pn=S1S2+S2S3+…+SnSn+1,Tn=b1b2+b2b3+…+bnbn+1,试求Tn,并证明Pn<
)+1.记Pn=S1S2+S2S3+…+SnSn+1,Tn=b1b2+b2b3+…+bnbn+1,试求Tn,并证明Pn<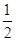 .
.
已知函数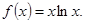
(1)求函数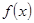 的极值点;
的极值点;
(2)若直线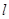 过点(0,—1),并且与曲线
过点(0,—1),并且与曲线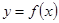 相切,求直线
相切,求直线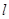 的方程;
的方程;
(3)设函数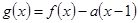 ,其中
,其中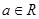 ,求函数
,求函数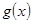 在
在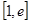 上的最小值.(其中e为自然对数的底数)
上的最小值.(其中e为自然对数的底数)
.
观察下表:
1,
2,3,
4,5,6,7,
8,9,10,11,12,13,14,15,
……
问:(1)此表第n行的第一个数与最后一个数分别是多少?
(2)此表第n行的各个数之和是多少?
(3)2012是第几行的第几个数?
.
如图,ABCD是菱形,PA⊥平面ABCD,PA=AD=2, BAD=60°.
BAD=60°.
(1)证明:面PBD⊥面PAC;
(2)求锐二面角A—PC—B的余弦值.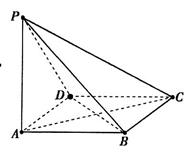
在△ABC中,角A,B,C的对边分别是a,b,c,已知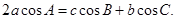
(1)求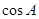 的值;
的值;
(2)若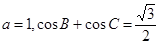 ,求边c的值.
,求边c的值.
.
设数列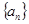 满足
满足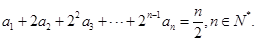
(1)求数列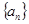 的通项公式;
的通项公式;
(2)设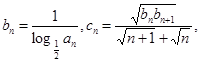 记
记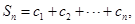 证明:Sn<1.
证明:Sn<1.