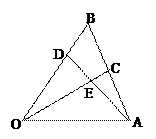 如图,已知ΔABO中,点C为线段AB中点,点D
如图,已知ΔABO中,点C为线段AB中点,点D
是线段OB上的点,且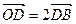 ,AD和OC交于点E,
,AD和OC交于点E,
设 .
.
(1)用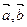 表示向量
表示向量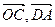 ;
;
(2)若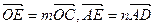 ,求实数
,求实数 的值.
的值.
某商店试销某种商品,获得如下数据:
| 日销售量(件) |
0 |
1 |
2 |
3 |
| 概率 |
0.05 |
0.25 |
0.45 |
0.25 |
试销结束后(假设该商品的日销售量的分布规律不变),设某天开始营业时有该商品3件,当天营业结束后检查存货,若发现存货少于2件,则当天进货再补充3件,否则不进货。
(Ⅰ)求当天商品不进货的概率;
(Ⅱ)记X为第二天开始营业时该商品的件数,求X的分布列和数学期望。
已知椭圆 ,直线l为圆
,直线l为圆 的一条切线,且经过椭圆C的右焦点,直线l的倾斜角为
的一条切线,且经过椭圆C的右焦点,直线l的倾斜角为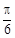 ,记椭圆C的离心率为e.
,记椭圆C的离心率为e.
(1)求e的值;
(2)试判定原点关于l的对称点是否在椭圆上,并说明理由。
已知在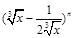 的展开式中,第6项
的展开式中,第6项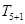 为常数项.
为常数项.
(1)求n;
(2)求展开式中所有的有理项.
某射手击中目标的概率为0.8,每次射击的结果相互独立,现射击10次,问他最有可能射中几次?
已知函数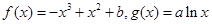 .
.
(1)若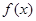 在
在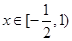 上的最大值为
上的最大值为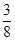 ,求实数
,求实数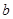 的值;
的值;
(2)若对任意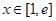 ,都有
,都有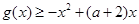 恒成立,求实数
恒成立,求实数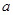 的取值范围;
的取值范围;
(3)在(1)的条件下,设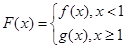 ,对任意给定的正实数
,对任意给定的正实数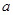 ,曲线
,曲线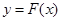 上是否存在两点
上是否存在两点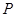 、
、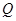 ,使得
,使得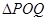 是以
是以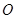 (
(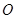 为坐标原点)为直角顶点的直角三角形,且此三角形斜边中点在
为坐标原点)为直角顶点的直角三角形,且此三角形斜边中点在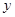 轴上?请说明理由。
轴上?请说明理由。