(本小题满分14分)
某慈善机构举办一次募捐演出,有一万人参加,每人一张门票,每张100元,在演出过程中穿插抽奖活动,第一轮抽奖从这一万张票根中随机抽取10张,其持有者获得价值1000元的奖品,并 参加第二轮抽奖活动,第二轮抽奖由第一轮获奖者独立操作按钮,电脑随机产生两个数
参加第二轮抽奖活动,第二轮抽奖由第一轮获奖者独立操作按钮,电脑随机产生两个数 ,如果
,如果 则电脑显示“中奖”,抽奖者获得9000元奖金;否则若电脑显示“谢谢”,则不中奖。
则电脑显示“中奖”,抽奖者获得9000元奖金;否则若电脑显示“谢谢”,则不中奖。
(I)已知小曹在第一轮抽奖中被抽中,求小曹在第二轮抽奖中获奖的概率;
(II)若小叶参加了此次活动,求小叶参加此次活动收益的期望;
(III)若此次募捐除奖品和奖金外,不计其它支出,该机构想获得96万元的慈善款,问该慈善机构此 次募捐是否能达到预期目标。
次募捐是否能达到预期目标。
选修4-5:不等式选讲
已知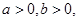 且
且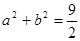 ,若
,若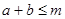 恒成立,
恒成立,
(Ⅰ)求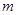 的最小值;
的最小值;
(Ⅱ)若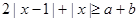 对任意的
对任意的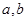 恒成立,求实数
恒成立,求实数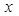 的取值范围.
的取值范围.
选修4-4:坐标系与参数方程
(Ⅰ)求直线 (
( 为参数)的倾斜角的大小.
为参数)的倾斜角的大小.
(Ⅱ)在极坐标系中,已知点 ,
, 是曲线
是曲线 上任意一点,求
上任意一点,求 的面积的最小值.
的面积的最小值.
选修4-2:矩阵与变换已知矩阵 ,向量
,向量 ,
,
(Ⅰ)求矩阵A的特征值和对应的特征向量;
(Ⅱ)求向量 ,使得
,使得 .
.
.已知函数
(Ⅰ)当 时,求
时,求 的值域
的值域
(Ⅱ)设 ,若
,若 在
在 恒成立,求实数a的取值范围
恒成立,求实数a的取值范围
(III)设 ,若
,若 在
在 上的所有极值点按从小到大排成一列
上的所有极值点按从小到大排成一列 ,
,
求证:
.(本小题满分13分)
以椭圆 :
: 的中心
的中心 为圆心,
为圆心, 为半径的圆称为该椭圆的“准圆”.设椭圆
为半径的圆称为该椭圆的“准圆”.设椭圆 的左顶点为
的左顶点为 ,左焦点为
,左焦点为 ,上顶点为
,上顶点为 ,且满足
,且满足 ,
, .
.
(Ⅰ)求椭圆 及其“准圆”的方程;
及其“准圆”的方程;
(Ⅱ)若椭圆 的“准圆”的一条弦
的“准圆”的一条弦 (不与坐标轴垂直)与椭圆
(不与坐标轴垂直)与椭圆 交于
交于 、
、 两点,试证明:当
两点,试证明:当 时,试问弦
时,试问弦 的长是否为定值,若是,求出该定值;若不是,请说明理由.
的长是否为定值,若是,求出该定值;若不是,请说明理由.