(本小题满分12分)函数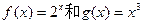 的图象的示意图如图所示,设
的图象的示意图如图所示,设
两函数的图象交于点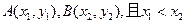
(1)请指出示意图中C1,C2分别对应哪一个函数? (2)若
(2)若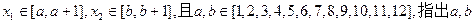 的值,并说明理由;
的值,并说明理由;
设命题 :函数
:函数 的定义域为
的定义域为 ;命题
;命题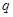 :当
:当 时,函数
时,函数 恒成立,如果命题“p∨q”为真命题,命题“p∧q”为假命题,求
恒成立,如果命题“p∨q”为真命题,命题“p∧q”为假命题,求 的取值范围.
的取值范围.
某校数学教师为调查本校2014届学生的高考数学成绩情况,用简单随机抽样的方法抽取20名学生的成绩,样本数据的茎叶图如图所示,但部分数据不小心丢失,同时得到如下所示的频率分布表:
| 分数段 |
 |
 |
 |
 |
 |
总计 |
| 频数 |
 |
|||||
| 频率 |
 |
 |

(1)求表中 的值及分数在
的值及分数在 范围内的学生人数,并估计这次考试全校学生数学成绩的及格率(分数在
范围内的学生人数,并估计这次考试全校学生数学成绩的及格率(分数在 内为及格);
内为及格);
(2)从大于等于110分的成绩中随机选2个成绩,求这2个成绩的平均分不小于130分的概率。
已知椭圆C的中心在原点,焦点在 轴上,焦距为2,离心率为
轴上,焦距为2,离心率为 .
.
(1)求椭圆C的方程;
(2)设直线l经过点M(0,1),且与椭圆C交于A,B两点,若 ,求直线l的方程.[
,求直线l的方程.[
对某班学生是爱好体育还是爱好文娱进行调查,根据调查得到的数据,所绘制的二维条形图如图.
(1)根据图中的数据,填好2×2列表,并计算在多大的程度上可以认为性别与是否爱好体育有关系:
(2)若已从男生中选出3人,女生中选出2人,从这5人中选出2人担任活动的协调人,求选出的两人性别相同的概率.
| 男 |
女 |
总计 |
|
| 爱好体育 |
|||
| 爱好文娱 |
|||
| 总计 |

参考数据:
 |
0.5 |
0.4 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
0.455 |
0.708 |
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
参考公式:
已知椭圆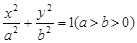 与
与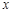 轴,
轴,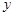 轴的正半轴分别交于A,B两点,原点O到直线AB的距离为
轴的正半轴分别交于A,B两点,原点O到直线AB的距离为 该椭圆的离心率为
该椭圆的离心率为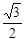
(1)求椭圆的方程
(2)是否存在过点P(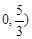 的直线
的直线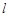 与椭圆交于M,N两个不同的点,使
与椭圆交于M,N两个不同的点,使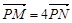 成立?若存在,求出
成立?若存在,求出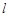 的方程;若不存在,说明理由。
的方程;若不存在,说明理由。