某校数学教师为调查本校2014届学生的高考数学成绩情况，用简单随机抽样的方法抽取20名学生的成绩，样本数据的茎叶图如图所示，但部分数据不小心丢失，同时得到如下所示的频率分布表：
| 分数段 |
 |
 |
 |
 |
 |
总计 |
| 频 数 |
|
|
|
 |
|
|
| 频 率 |
 |
 |
|
|
|
|
（1）求表中
的值及分数在
范围内的学生人数，并估计这次考试全校学生数学成绩的及格率（分数在
内为及格）；
（2）从大于等于110分的成绩中随机选2个成绩，求这2个成绩的平均分不小于130分的概率。
已知抛物线
，
（1）用配方法确定它的顶点坐标、对称轴；
（2）
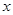取何值时，
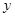随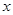增大而减小？
（3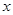）取何值时，抛物线在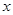轴上方？
在△ABC中，AB=AC=5，BC=6，求cosB、sinA
当a＞0且x＞0时，因为
，所以
，从而
（当x＝
时取等号）．记函数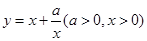
，由上述结论可知：当x＝时，该函数有最小值为2
（1）已知函数y1=x（x＞0）与函数
，则当x=时，y1+y2取得最小值为
（2）已知函数y1=x+1（x＞-1）与函数y2＝（x+1）2+4（x＞−1），求
的最小值，并指出取得该最小值时相应的x的值．
如图是一个圆锥与其侧面展开图，已知圆锥的底面半径是2，母线长是6.
（1）求这个圆锥的高和其侧面展开图中∠ABC的度数；
（2）如果A是底面圆周上一点，从点A拉一根绳子绕圆锥侧面一圈再回到A点，求这根绳子的最短长度．
已知点P（1，-2a）在二次函数y=ax2+6的图象上，并且点P关于x轴的对称点在反比例函数
的图象上。
（1）求此二次函数和反比例函数的解析式；
（2）点（-1，4）是否同时在（1）中的两个函数图象上？