当a＞0且x＞0时，因为
，所以
，从而
（当x＝
时取等号）．记函数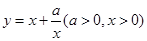
，由上述结论可知：当x＝时，该函数有最小值为2
（1）已知函数y1=x（x＞0）与函数
，则当x= 时，y1+y2取得最小值为
（2）已知函数y1=x+1（x＞-1）与函数y2＝（x+1）2+4（x＞−1），求
的最小值，并指出取得该最小值时相应的x的值．
2010年世博会于5月1日在中国上海隆重开幕，甲、乙、丙三人打算利用周六去游览，由于时间有限，三人商定在已圈定的10个国家馆中各自随机选择一个国家馆游览（选择每个国家馆的可能性相同）．
（Ⅰ）求甲、乙、丙三人同时游览同一个国家馆的概率；
（Ⅱ）求甲、乙、丙三人中至少有两人同时游览同一个国家馆的概率.
已知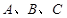
为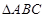
的三内角，且其对边分别为
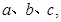若
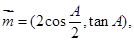
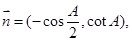且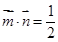
．
（Ⅰ）求角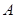
；
（Ⅱ）若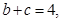
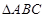的面积为
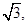求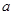
．
定义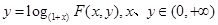
，
（Ⅰ）令函数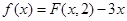
，过坐标原点O作曲线C：
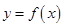的切线
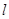，切点为P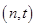
（n>0），设曲线C与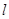及y轴围成图形的面积为S，求S的值。
（Ⅱ）令函数
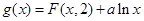,讨论函数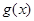
是否有极值，如果有，说明是极大值还是极小值。
（Ⅲ）证明：当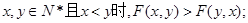
如图，在三棱锥S—ABC中，SC⊥平面ABC，点P、M分别是SC和SB的中点，设
PM=AC=1，∠ACB=90°，直线AM与直线SC所成的角为60°．
（I）求证：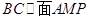
；（Ⅱ）求证：平面MAP⊥平面SAC；
（ Ⅲ）求锐二面角M—AB—C的大小的余弦值；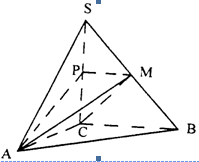
3个同学分别从a，b，c，d四门校本课程中任选其中一门，每个同学选哪一门互不影响；（I）求3个同学选择3门不同课程的概率；（II）求恰有2门课程没有被选择的概率；（Ⅲ）求选择课程a的同学个数的分布列及数学期望.