已知四棱锥
的底面为直角梯形，
，
底面
，且
，
，
是
的中点。
（Ⅰ）证明：面
面
；
（Ⅱ）求
与
所成角的余弦值；
（Ⅲ）求面
与面
所成二面角的余弦值。
如图，四棱锥P-ABCD中，底面ABCD为矩形，平面PAD⊥平面ABCD.
（1）求证：AB⊥PD；
（2）若M为PC的中点，求证：PA∥平面BDM.
（本小题满分14分）已知函数
．
（1）求
的最小正周期；
（2）若将的图像向右平移
个单位，得到函数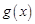
的图像，求函数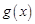在区间
上的最大值和最小值．
（本小题满分16分）已知函数
有且只有一个零点，其中a＞0.
（1）求a的值；
（2）若对任意的
，有
恒成立，求实数k的最小值；
（3）设
，对任意
，
证明：不等式
恒成立.
（本小题满分16分）已知函数
．
（1）若
，解方程
；
（2）若函数
在
上单调递增，求实数
的取值范围；
（3）若函数在
上的最小值为6，求实数的值．
如图，在平面直角坐标系
中，已知四边形
是等腰梯形，
，点
满足
，点
在线段
上运动（包括端点）.
（1）求
的余弦值；
（2）是否存在实数
，使
，若存在，求出满足条件的实数的取值范围，若不存在，请说明理由.