如图,四棱锥P-ABCD中,底面ABCD为矩形,平面PAD⊥平面ABCD.
(1)求证:AB⊥PD;
(2)若M为PC的中点,求证:PA∥平面BDM.
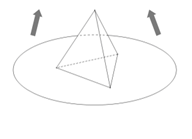
(本小题满分14分)某商场为促销要准备一些正三棱锥形状的装饰品,用半径为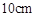 的圆形包装纸包装.要求如下:正三棱锥的底面中心与包装纸的圆心重合,包装纸不能裁剪,沿底边向上翻折,其边缘恰好达到三棱锥的顶点,如图所示.设正三棱锥的底面边长为
的圆形包装纸包装.要求如下:正三棱锥的底面中心与包装纸的圆心重合,包装纸不能裁剪,沿底边向上翻折,其边缘恰好达到三棱锥的顶点,如图所示.设正三棱锥的底面边长为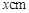 ,体积为
,体积为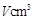 .
.
(1)求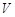 关于
关于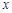 的函数关系式;
的函数关系式;
(2)在所有能用这种包装纸包装的正三棱锥装饰品中,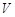 的最大值是多少?并求此时
的最大值是多少?并求此时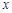 的值.
的值.
(本小题满分14分)如图,在斜三棱柱 中,侧面
中,侧面 是边长为
是边长为 的菱形,
的菱形, .在面
.在面 中,
中,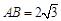 ,
,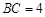 ,
, 为
为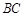 的中点,过
的中点,过 三点的平面交
三点的平面交 于点
于点 .
.
(1)求证: 为
为 中点;
中点;
(2)求证:平面 平面
平面 .
.
(本小题满分14分)在 中,
中, ,
, .
.
(1)求 的值;
的值;
(2)若 ,求
,求 的面积.
的面积.
(本小题满分14分)已知函数 ,且对任意
,且对任意 ,都有
,都有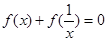 .
.
(1)求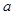 ,
,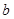 的关系式;
的关系式;
(2)若 存在两个极值点
存在两个极值点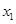 ,
, ,且
,且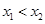 ,求出
,求出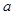 的取值范围并证明
的取值范围并证明 ;
;
(3)在(2)的条件下,判断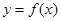 零点的个数,并说明理由.
零点的个数,并说明理由.
(本小题满分14分)已知平面上的动点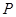 与点
与点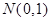 连线的斜率为
连线的斜率为 ,线段
,线段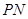 的中点与原点连线的斜率为
的中点与原点连线的斜率为 ,
, (
( ),动点
),动点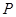 的轨迹为
的轨迹为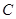 .
.
(1)求曲线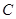 的方程;
的方程;
(2)恰好存在唯一一个同时满足以下条件的圆:
①以曲线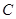 的弦
的弦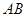 为直径;
为直径;
②过点 ;
;
③直径 .求
.求 的取值范围.
的取值范围.