（本小题满分14分）已知函数
，且对任意
，都有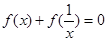
.
（1）求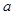
，
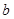的关系式；
（2）若
存在两个极值点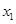
，
，且
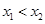，求出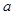的取值范围并证明
；
（3）在（2）的条件下，判断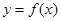
零点的个数，并说明理由．
已知多面体
中， 四边形
为矩形，
，
，平面
平面， 
、
分别为
、
的中点，且
，
.
（1）求证：
平面
；
（2）求证：
平面
；
（3）设平面
将几何体
分成的两个锥体的体积分别为
，
，求
的值.
已知函数
．
（1）若
在
上存在零点，求实数
的取值范围；
（2）当
时，若对任意的
，总存在
使
成立，求实数
的取值范围．
如图，椭圆
过点P(1, 
)，其左、右焦点分别为F1,F2,离心率e＝
, M, N是直线x＝4上的两个动点，且
·
＝0.
（1）求椭圆的方程；
（2）求MN的最小值；
（3）以MN为直径的圆C是否过定点？
已知函数f(x)＝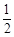
ax2－(2a＋1)x＋2lnx(a∈R).
（1）若曲线y＝f(x)在x＝1和x＝3处的切线互相平行，求a的值；
（2）当a≤0时，求f(x)的单调区间。
已知函数y＝x－1，令x＝―4,―3,―2,－1,0,1,2,3,4，可得函数图象上的九个点，在这九个点中随机取出两个点P1(x1,y1),P2(x2,y2)，
（1）求P1,P2两点在双曲线xy＝6上的概率；
（2）求P1,P2两点不在同一双曲线xy＝k(k≠0)上的概率。