(本小题满分14分)如图,在斜三棱柱 中,侧面
中,侧面 是边长为
是边长为 的菱形,
的菱形, .在面
.在面 中,
中,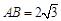 ,
,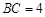 ,
, 为
为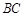 的中点,过
的中点,过 三点的平面交
三点的平面交 于点
于点 .
.
(1)求证: 为
为 中点;
中点;
(2)求证:平面 平面
平面 .
.
(本小题满分12分)海中有 岛,已知
岛,已知 岛
岛 四周
四周 海里内有暗礁,现一货轮由
海里内有暗礁,现一货轮由
西向东航行,在 处望见
处望见 岛在北偏东
岛在北偏东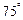 ,再航行
,再航行 海里到
海里到 后,见
后,见 岛在北偏东
岛在北偏东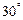 ,
,
如货轮不改变航向继续航行,有无触礁的危险?
(本 小题满分12分)在△ABC中, a, b, c分别为角A, B, C所对的边,
小题满分12分)在△ABC中, a, b, c分别为角A, B, C所对的边,
且4sin2 -cos2A=
-cos2A= .
.
(1)求角A的度数; (2)若a=
(2)若a= , b+c=3,求b和c的值.
, b+c=3,求b和c的值.
(本小题满分1 0分)在等
0分)在等 比数列
比数列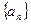 中,
中,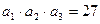 ,
,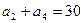
试求:(1)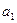 和公比
和公比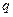 ;(2)前6项的和
;(2)前6项的和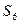 .
.
已知 ,且
,且 (
( 为自然对数的底数)。
为自然对数的底数)。
(1)求 与
与 的关系;
的关系;
(2)若 在其定义域内为增函数,求
在其定义域内为增函数,求 的取值范围;
的取值范围;
(3)证明:
(提示:需要时可利用恒等式: )
)
(本小题满分15分)已知函数 ,
,
(Ⅰ)判断函数
 的
的 奇偶性;
奇偶性;
(Ⅱ)求函数 的单调区间;
的单调区间;
(Ⅲ)若关于 的方程
的方程 在
在 上有实数解,求实数
上有实数解,求实数 的取值范围.
的取值范围.