(本小题满分12分)
已知函数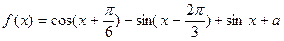 的最大值为
的最大值为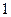 .
.
(1)求常数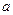 的值;
的值;
(2)求使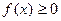 成立的
成立的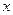 的取值范围.
的取值范围.
..(本小题满分14分)定义在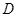 上的函数
上的函数 ,如果满足;对任意
,如果满足;对任意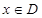 ,存在常数
,存在常数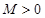 ,都有
,都有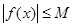 成立,则称
成立,则称 是
是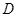 上的有界函数,其中
上的有界函数,其中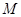 称为函数
称为函数 的上界.已知函数
的上界.已知函数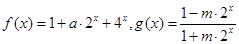 .
.
(Ⅰ)当 时,求函数
时,求函数 在
在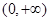 上的值域,并判断函数
上的值域,并判断函数 在
在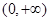 上是否为有界函数,请说明理由;
上是否为有界函数,请说明理由;
(Ⅱ)若 是
是 上的有界函数,且
上的有界函数,且 的上界为3,求实数
的上界为3,求实数 的取值范围;
的取值范围;
(Ⅲ)若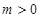 ,求函数
,求函数 在
在 上的上界
上的上界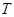 的取值范围.
的取值范围.
..(本小题满分14分)坐标法是解析几何中最基本的研究方法,坐标法是以坐标系为桥梁,把几何问题转化成代数问题,通过代数运算研究几何图形性质的方法.请利用坐标法解决以下问题:
(Ⅰ)在直角坐标平面内,已知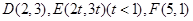 ,对任意
,对任意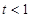 ,试判断
,试判断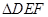 的形状;
的形状;
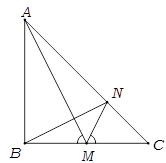
(Ⅱ)在平面内,已知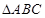 中,
中,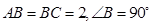 ,
,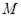 为
为 的中点,
的中点,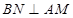 交
交 于
于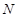 ,求证:
,求证: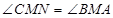 .
.
.(本小题满分13分)一个几何体的直观图及三视图如图所示,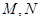 分别是
分别是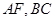 的中点.
的中点.
(Ⅰ)写出这个几何体的名称;
(Ⅱ)求证: ;
;
(Ⅲ)求多面体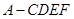 的体积.
的体积.
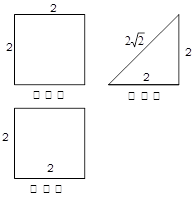
.(本小题满分13分)汽车和自行车分别从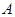 地和
地和 地同时开出,如下图,各沿箭头方向(两方向垂直)匀速前进,汽车和自行车的速度分别是10米/秒和5米/秒,已知
地同时开出,如下图,各沿箭头方向(两方向垂直)匀速前进,汽车和自行车的速度分别是10米/秒和5米/秒,已知 米.(汽车开到
米.(汽车开到 地即停止)
地即停止)
(Ⅰ)经过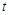 秒后,汽车到达
秒后,汽车到达 处,自行车到达
处,自行车到达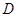 处,设
处,设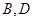 间距离为
间距离为 ,试
,试
写出 关于
关于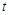 的函数关系式,并求其定义域.
的函数关系式,并求其定义域.
(Ⅱ)经过多少时间后,汽车和自行车之间的距离最短?最短距离是多少?
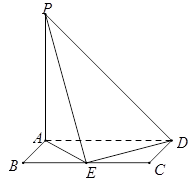
.(本小题满分13分)已知 是矩形,
是矩形, 平面
平面 ,
,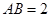 ,
, ,
,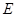 为
为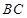 的中点.
的中点.
(Ⅰ)求证: 平面
平面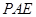 ;
;
(Ⅱ)求直线 与平面
与平面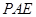 所成的角.
所成的角.