在平面直角坐标系中，如图1，将n个边长为1的正方形并排组成矩形OABC，相邻两边OA和OC分别落在x轴和y轴的正半轴上，设抛物线y=ax2+bx+c（a＜0）过矩形顶点B、C．
（1）当n=1时，如果a=﹣1，试求b的值；
（2）当n=2时，如图2，在矩形OABC上方作一边长为1的正方形EFMN，使EF在线段CB上，如果M，N两点也在抛物线上，求出此时抛物线的解析式；
（3）将矩形OABC绕点O顺时针旋转，使得点B落到x轴的正半轴上，如果该抛物线同时经过原点O．
①试求当n=3时a的值；
②直接写出a关于n的关系式．
如图所示，在△ABC中，AB=AC，∠C=30°，AB⊥AD，AD=4cm，求BC的长．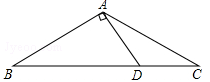
如图，△ABC中，∠A = 40°，∠B = 72°，CE平分∠ACB，CD⊥AB于D，DF⊥CE，求∠CDF度数．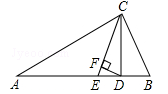
如图，在平面直角坐标系中，A（﹣1，5），B（﹣1，0），C（﹣4，3）．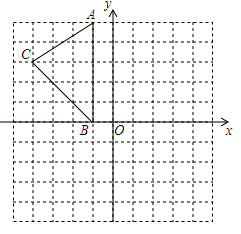
（1）在图中作出△ABC关于y轴的对称图形△A1B1C1；
（2）在y轴上找出一点P，使的PA+PB的值最小，直接画出点P的位置．
完成下列各题
（1）计算：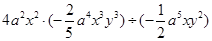
；
（2）计算：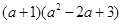
；
（3）因式分解：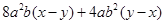
．
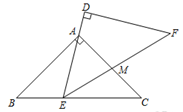
如图，△ABC与△DEF是两个全等的等腰直角三角形，∠BAC=∠D=90°，AB=AC=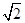
．现将△DEF与△ABC按如图所示的方式叠放在一起．现将△ABC保持不动，△DEF运动，且满足：点E在边BC上运动（不与B、C重合），且边DE始终经过点A，EF与AC交于M点．请问：在△DEF运动过程中，△AEM能否构成等腰三角形？若能，请求出BE的长；若不能，请说明理由．