(本小题满分12分)
对某电子元件进行寿命追踪调查,情况如下:
| 寿命/小时 |
100~200 |
200~300 |
300~400 |
400~500 |
500~600 |
| 个数 |
20 |
30 |
80 |
40 |
30 |
(1)完成频率分布表;
| 分组 |
频数 |
频率 |
| 100~200 |
|
|
| 200~300 |
|
|
| 300~400 |
|
|
| 400~500 |
|
|
| 500~600 |
|
|
| 合计 |
|
|
(2)画出频率分布直方图和频率分布折线图;
(3)估计电子元件寿命在100~400小时以内的频率;
已知函数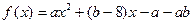 ,当
,当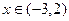 时f(x)>0,
时f(x)>0,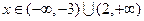 时f(x)<0
时f(x)<0
(1)求y=f(x)的解析式;
(2)c为何值时,不等式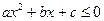 的解集为R.
的解集为R.
经市场调查,某种商品在过去50天的销售和价格均为销售时间t(天)的函数,且销售量近似地满足f (t) =" –" 2t + 200(1 ≤ t ≤ 50 , t ∈ N ),前30天价格为g (t) = 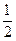 t + 30 (1 ≤ t ≤ 30 , t ∈ N ),后20天价格为g (t) =" 45" (31 ≤ t ≤ 50 , t ∈ N ).
t + 30 (1 ≤ t ≤ 30 , t ∈ N ),后20天价格为g (t) =" 45" (31 ≤ t ≤ 50 , t ∈ N ).
(1)写出该种商品的日销售S与时间t的函数关系;
(2)求日销售S的最大值.
佛山某公司生产陶瓷,根据历年的情况可知,生产陶瓷每天的固定成本为14000元,每生产一件产品,成本增加210元.已知该产品的日销售量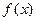 与产量
与产量 之间的关系式为
之间的关系式为 ,每件产品的售价
,每件产品的售价 与产量
与产量 之间的关系式为
之间的关系式为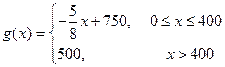 .
.
(Ⅰ)写出该陶瓷厂的日销售利润 与产量
与产量 之间的关系式;
之间的关系式;
(Ⅱ)若要使得日销售利润最大,每天该生产多少件产品,并求出最大利润.
已知函数f(x)的定义域为{x| x ≠ kπ,k ∈ Z},且对于定义域内的任何x、y,有f(x-y) = 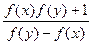 成立,且f(a) = 1(a为正常数),当0 < x < 2a时,f(x) > 0.(I)判断f(x)奇偶性;(II)证明f(x)为周期函数;(III)求f(x)在[2a,3a] 上的最小值和最大值.
成立,且f(a) = 1(a为正常数),当0 < x < 2a时,f(x) > 0.(I)判断f(x)奇偶性;(II)证明f(x)为周期函数;(III)求f(x)在[2a,3a] 上的最小值和最大值.
某机床厂今年年初用98万元购进一台数控机床,并立即投入生产使用,计划第一年维修、保养费用12万元,从第二年开始,每年所需维修、保养费用比上一年增加4万元,该机床使用后,每年的总收入为50万元,设使用x年后数控机床的盈利额为y万元.
(1)写出y与x之间的函数关系式;
(2)从第几年开始,该机床开始盈利(盈利额为正值)
(3)使用若干年后,对机床的处理方案有两种:(Ⅰ)当年平均盈利额达到最大值时,以30万元价格处理该机床;(Ⅱ)当盈利额达到最大值时,以12万元价格处理该机床.
请你研究一下哪种方案处理较为合理?请说明理由.