某机床厂今年年初用98万元购进一台数控机床,并立即投入生产使用,计划第一年维修、保养费用12万元,从第二年开始,每年所需维修、保养费用比上一年增加4万元,该机床使用后,每年的总收入为50万元,设使用x年后数控机床的盈利额为y万元.
(1)写出y与x之间的函数关系式;
(2)从第几年开始,该机床开始盈利(盈利额为正值)
(3)使用若干年后,对机床的处理方案有两种:(Ⅰ)当年平均盈利额达到最大值时,以30万元价格处理该机床;(Ⅱ)当盈利额达到最大值时,以12万元价格处理该机床.
请你研究一下哪种方案处理较为合理?请说明理由.
已知在直角坐标系xOy中,直线l的参数方程为 ,(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ2﹣4ρcosθ+3=0.
,(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ2﹣4ρcosθ+3=0.
(Ⅰ)求直线l的普通方程和曲线C的直角坐标方程;
(Ⅱ)设点P是曲线C上的一个动点,求它到直线l的距离d的取值范围.
如图,AB是的⊙O直径,CB与⊙O相切于B,E为线段CB上一点,连接AC、AE分别交⊙O于D、G两点,连接DG交CB于点F.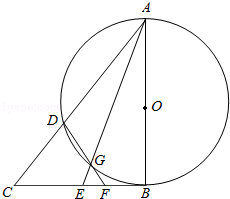
(Ⅰ)求证:C、D、G、E四点共圆.
(Ⅱ)若F为EB的三等分点且靠近E,EG=1,GA=3,求线段CE的长.
已知f(x)=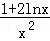 .
.
(1)求f(x)的单调区间;
(2)令g(x)=ax2﹣2lnx,则g(x)=1时有两个不同的根,求a的取值范围;
(3)存在x1,x2∈(1,+∞)且x1≠x2,使|f(x1)﹣f(x2)|≥k|lnx1﹣lnx2|成立,求k的取值范围.
已知椭圆C: +
+ =1(a>b>0)的下顶点为P(0,﹣1),P到焦点的距离为
=1(a>b>0)的下顶点为P(0,﹣1),P到焦点的距离为 .
.
(Ⅰ)设Q是椭圆上的动点,求|PQ|的最大值;
(Ⅱ)若直线l与圆O:x2+y2=1相切,并与椭圆C交于不同的两点A、B.当 •
• =λ,且满足
=λ,且满足 ≤λ≤
≤λ≤ 时,求△AOB面积S的取值范围.
时,求△AOB面积S的取值范围.
如图,三棱柱ABC﹣A1B1C1中,AA1⊥平面ABC,∠BAC=90°,AB=2,AC=6,点D在线段BB1上,且BD= ,A1C∩AC1=E.
,A1C∩AC1=E.
(Ⅰ)求证:直线DE与平面ABC不平行;
(Ⅱ)设平面ADC1与平面ABC所成的锐二面角为θ,若cosθ= ,求AA1的长;
,求AA1的长;
(Ⅲ)在(Ⅱ)的条件下,设平面ADC1∩平面ABC=l,求直线l与DE所成的角的余弦值.