某日用品按行业质量标准分成五个等级，等级系数X依次为1，2，3，4，5．现从一批该日用品中随机抽取20件，对其等级系数进行统计分析，得到频率分布表如下：
| 1 |
2 |
3 |
4 |
5 |
|
| 0.2 |
0.45 |
（Ⅰ）若所抽取的20件日用品中，等级系数为4的恰有3件，等级系数为5的恰有2件，求、、的值；
（Ⅱ）在（Ⅰ）的条件下，将等级系数为4的3件日用品记为，，，等级系数为5的2件日用品记为，，现从，，，，这5件日用品中任取两件（假定每件日用品被取出的可能性相同），写出所有可能的结果，并求这两件日用品的等级系数恰好相等的概率．
矩形ABCD，AB=3，BC=4，沿对角线BD把△ABD折起，使点A在平面BCD上的射影A′落在BC上，求二面角A-BD-C的大小的余弦值．
在高中阶段，在各个领域我们学习许多知识．在语言与文学领域，学习语文和外语；在数学领域学习数学；在人文与社会领域，学习思想政治、历史和地理；在科学领域，学习物理、化学和生物；在技术领域，学习通用技术和信息技术；在艺术领域学习音乐、美术和艺术；在体育与健康领域，学习体育等．试设计一个学习知识结构图．
设
是集合
中所有的数从小到大排列成的数列，即
，
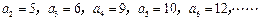将数列各项按照上小下大，左小右大的原则写成如下的三角形数表：
（1）写出这个三角形数表的第四行、第五行；
（2）求
．
某运动员训练次数与训练成绩之间的数据关系如下：
| 次数（x） |
30 |
33 |
35 |
37 |
39 |
44 |
46 |
50 |
| 成绩（y） |
30 |
34 |
37 |
39 |
42 |
46 |
48 |
51 |
⑴在图1坐标系中做出散点图；
⑵求出回归方程；
⑶计算相关系数，并利用其检验两个变量的相关关系的显著性；
⑷在图2中做出残差图；
⑸计算相关指数
；
⑹试预测该运动员训练47次及55次的成绩.
（本小题满分
分）某同学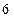
次考试的数学
、语文
成绩在班中的排名如下表：
| 数学成绩 |
 |
 |
 |
 |
 |
 |
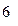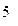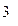| 语文成绩 |
 |
 |
 |
|
 |
|
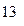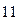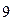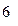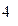对上述数据分别用
与
来拟合
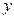与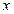
之间的关系，并用残差分析两者的拟合效果.