(本小题满分12分)为了解高一年级学生的基本数学素养,某中学特地组织了一次数学基础知识竞赛,随机抽取统测成绩得到一样本.其分组区间和频数是:  ,
,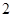 ;
;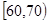 ,
,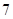 ;
; ,
,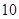 ;
;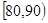 ,
,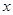 ; [90,100],
; [90,100],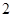 . 其频率分布直方图受到破坏,可见部分如下图所示,据此解答如下问题.
. 其频率分布直方图受到破坏,可见部分如下图所示,据此解答如下问题.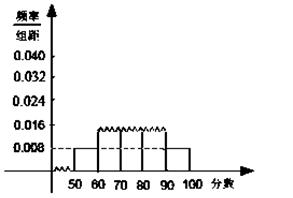
(1)求样本的人数及x的值;
(2)估计样本的众数,并计算频率分布直方图中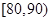 的矩形的高;
的矩形的高;
(3)从成绩不低于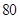 分的样本中随机选取
分的样本中随机选取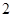 人,该
人,该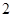 人中成绩在
人中成绩在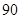 分以上(含
分以上(含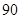 分)的人数记为
分)的人数记为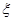 ,求
,求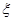 的分布列及其数学期望.
的分布列及其数学期望.
已知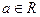 ,
,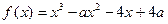 .
.
(I)若 ,求函数
,求函数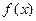 在区间
在区间 的最大值与最小值;
的最大值与最小值;
(II)若函数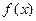 在区间
在区间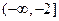 和
和 上都是增函数,求实数
上都是增函数,求实数 的取值范围.
的取值范围.
某家具城进行促销活动,促销方案是:顾客每消费1000元,便可以获得奖券一张,每张奖券中奖的概率为 ,若中奖,则家具城返还顾客现金200元. 某顾客购买一张价格为3400元的餐桌,得到3张奖券.
,若中奖,则家具城返还顾客现金200元. 某顾客购买一张价格为3400元的餐桌,得到3张奖券.
(I)求家具城恰好返还该顾客现金200元的概率;
(II)(文科)求家具城至少返还该顾客现金200元的概率.
(理科)设该顾客有 张奖券中奖,求
张奖券中奖,求 的分布列,并求
的分布列,并求 的数学
的数学
期望E.
在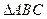 中,a、b、c分别为角A、B、C的对边,且满足
中,a、b、c分别为角A、B、C的对边,且满足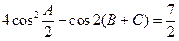
(I)求角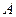 大小;
大小;
(II)若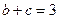 ,当
,当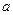 取最小值时,求
取最小值时,求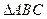 的面积.
的面积.
如图,四棱锥
中,底面
为矩形,
,
,
,
在侧棱
上,
.
(I)证明:
是侧棱
的中点;
(Ⅱ)求二面角
的大小.
在数列 中,
(I)设
,求数列
的通项公式;
(II)求数列
的前
项和
.