(本小题满分12分)
如图,函数y=2sin(πx+φ),x∈R,(其中0≤φ≤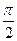 )的图象与y轴交于点(0,1)。 (1)求φ的值;(2)若
)的图象与y轴交于点(0,1)。 (1)求φ的值;(2)若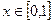 ,求函数y=2sin(πx+φ)的最值,及取得最值时
,求函数y=2sin(πx+φ)的最值,及取得最值时 的值;(3)设P是图象上的最高点,M、N是图象与x轴的交点,求
的值;(3)设P是图象上的最高点,M、N是图象与x轴的交点,求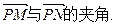 的余弦值。
的余弦值。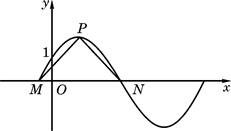
为了解甲、乙两种离子在小鼠体内的残留程度,进行如下试验:将200只小鼠随机分成 两组,每组100只,其中 组小鼠给服甲离子溶液, 组小鼠给服乙离子溶液.每只小鼠给服的溶液体积相同、摩尔浓度相同.经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比.根据试验数据分别得到如下直方图:

记 为事件:"乙离子残留在体内的百分比不低于 ",根据直方图得到 的估计值为 .
(1)求乙离子残留百分比直方图中 的值;
(2)分别估计甲、乙离子残留百分比的平均值(同一组中的数据用该组区间的中点值为代表).
已知数列 满足 .
证明: 当 时,
( I ) ;
( II ) ;
( III ) .
如图,已知抛物线 , 点 , 抛物线上的点
过点 作直线 的垂线,垂足为 .
( I ) 求直线 斜率的取值范围;
( II ) 求 的最大值。

已知函数 .
( I ) 求 的导函数;
( II ) 求 在区间 上的取值范围.
如图,已知四棱锥 是以 为斜边的等腰直角三角形, , 为 的中点.
(I ) 证明: 平面 ;
( II )求直线 与平面 所成角的正弦值.
