有3张扑克牌,分别是红桃3、红桃4和黑桃5.把牌洗匀后甲先抽取一
张,记下花色和数字后将牌放回,洗匀后乙再抽取一张.
⑴先后两次抽得的数字分别记为s和t,则︱s-t︱≥1的概率.
⑵甲、乙两人做游戏,现有两种方案.A方案:若两次抽得相同花色则甲胜,否则乙胜.B方案:若两次抽得数字和为奇数则甲胜,否则乙胜.
请问甲选择哪种方案胜率更高?
已知抛物线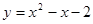 。
。<1>求抛物线顶点M的坐标;
<2>若抛物线与x轴的交点分别为点A、B(点A在点B的左边),与y轴交于点C,点N为线段BM上的一点,过点N作x轴的垂线,垂足为点Q.当点N在线段BM上运动时(点N不与点B,点M重合),设NQ的长为t,四边形NQAC的面积为S,求S与t之间的函数关系式及自变量t的取值范围;
<3>在对称轴右侧的抛物线上是否存在点P,使△PAC为直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.
我们知道三角形三条中线的交点叫做三角形的重心.经过证明我们可得三角形重心具备下面的性质: 重心到顶点的距离与重心到该顶点对边中点的距离之比为2﹕1.请你用此性质解决下面的问题.
已知:如图,点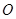 为等腰直角三角形
为等腰直角三角形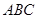 的重心,
的重心,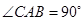 ,直线
,直线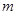 过点
过点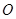 ,过
,过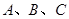 三点分别作直线
三点分别作直线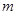 的垂线,垂足分别为点
的垂线,垂足分别为点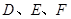 .
.
<1>当直线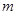 与
与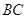 平行时(图1),请你猜想线段
平行时(图1),请你猜想线段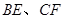 和
和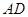 三者之间的数量关系并证明;
三者之间的数量关系并证明;
<2>当直线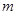 绕点
绕点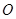 旋转到与
旋转到与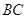 不平行时,分别探究在图2、图3这两种情况下,上述结论是否还成立?若成立,请给予证明;若不成立,线段
不平行时,分别探究在图2、图3这两种情况下,上述结论是否还成立?若成立,请给予证明;若不成立,线段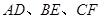 三者之间又有怎样的数量关系?请写出你的结论,不需证明.
三者之间又有怎样的数量关系?请写出你的结论,不需证明.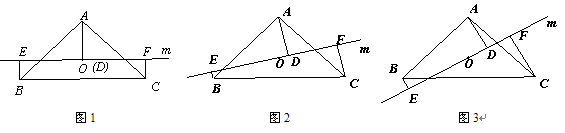
已知: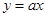 与
与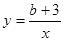 两个函数图象交点为
两个函数图象交点为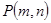 ,且
,且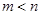 ,
,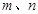 是关于
是关于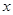 的一元二次方程
的一元二次方程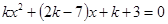 的两个不等实根,其中
的两个不等实根,其中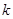 为非负整数.
为非负整数.<1>求
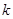 的值;
的值;<2>求
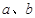 的值;
的值;<3>如果直线
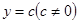 与函数
与函数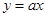 和
和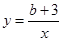 分别交于
分别交于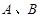 两点(点
两点(点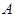 在点
在点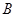 的左侧),线段
的左侧),线段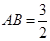 ,求
,求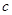 的值.
的值.
、在边长为1的正方形网格中,正方形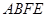 与正方形
与正方形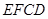 的位置如图所示.
的位置如图所示.
(1)请你按下列要求画图:
①联结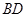 交
交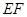 于点
于点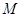 ;
;
②在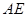 上取一点
上取一点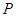 ,联结
,联结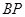 ,
,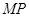 ,使△
,使△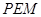 与△
与△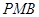 相似;
相似;(2)若
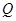 是线段
是线段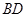 上一点,连结
上一点,连结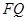 并延长交四边形
并延长交四边形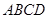 的一边于点
的一边于点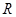 ,且满足
,且满足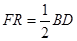 ,则
,则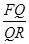 的值为_____________.
的值为_____________.
如图,在等腰梯形ABCD中,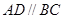 ,
,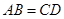 ,
,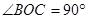 ,
,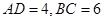
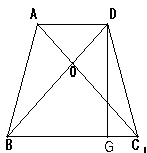 |
<1>过D作
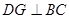 于G,则DG为梯形的高,求这个高DG;
于G,则DG为梯形的高,求这个高DG;<2>求
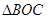 的面积。
的面积。