我们知道三角形三条中线的交点叫做三角形的重心.经过证明我们可得三角形重心具备下面的性质: 重心到顶点的距离与重心到该顶点对边中点的距离之比为2﹕1.请你用此性质解决下面的问题.
已知:如图,点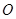 为等腰直角三角形
为等腰直角三角形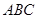 的重心,
的重心,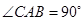 ,直线
,直线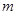 过点
过点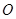 ,过
,过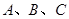 三点分别作直线
三点分别作直线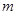 的垂线,垂足分别为点
的垂线,垂足分别为点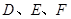 .
.
<1>当直线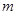 与
与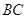 平行时(图1),请你猜想线段
平行时(图1),请你猜想线段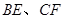 和
和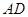 三者之间的数量关系并证明;
三者之间的数量关系并证明;
<2>当直线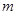 绕点
绕点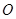 旋转到与
旋转到与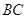 不平行时,分别探究在图2、图3这两种情况下,上述结论是否还成立?若成立,请给予证明;若不成立,线段
不平行时,分别探究在图2、图3这两种情况下,上述结论是否还成立?若成立,请给予证明;若不成立,线段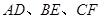 三者之间又有怎样的数量关系?请写出你的结论,不需证明.
三者之间又有怎样的数量关系?请写出你的结论,不需证明.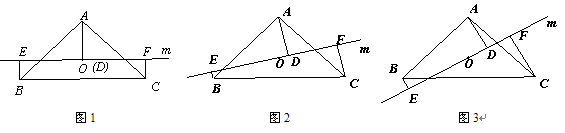
甲、乙两位同学玩转盘游戏,游戏规则:将圆盘平均分成三份,分别涂上红,黄,绿三种颜色,两位同学分别转动转盘两次(若压线,重新转).若两次指针指到的颜色相同,则甲获胜;若两次指针指到的颜色是黄绿组合则乙获胜;其余情况则视为平局.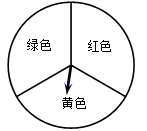
(1)请用画树状图的方法,列出所有可能出现的结果;
(2)试用概率说明游戏是否公平.
已知:如图,△ABD中,AC⊥BD于C,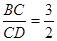 ,E是AB的中点,tanD=2,CE=1,求sin∠ECB和AD的长.
,E是AB的中点,tanD=2,CE=1,求sin∠ECB和AD的长.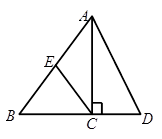
一次函数 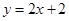 与反比例函数
与反比例函数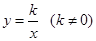 的图象都过点A
的图象都过点A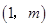 ,
,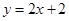 的图象与
的图象与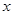 轴交于点B.
轴交于点B.
(1)求点B坐标及反比例函数的表达式;
(2)C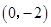 是
是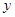 轴上一点,若四边形ABCD是平行四边形,直接写出点D的坐标,并判断D点是否在此反比例函数的图象上,并说明理由.
轴上一点,若四边形ABCD是平行四边形,直接写出点D的坐标,并判断D点是否在此反比例函数的图象上,并说明理由.
已知:如图,在△ABC中,BC=2, ,∠ABC=135°,求AC和AB的长.
,∠ABC=135°,求AC和AB的长.
如图,⊙O与割线AC交于点B,C,割线AD过圆心O,且∠DAC=30°.若⊙O的半径OB=5,AD=13,求弦BC的长.