已知 ,
,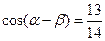 ,且
,且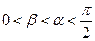 ,
,
(1)求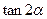 (2)求
(2)求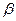
如图,已知三棱锥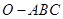 的侧棱
的侧棱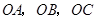 两两垂直,且
两两垂直,且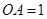 ,
, ,
, 是
是 的中点.
的中点.
(1)求异面直线 与
与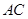 所成的角的余弦值
所成的角的余弦值
(2)求二面角 的余弦值
的余弦值
(3)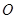 点到面
点到面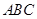 的距离
的距离
先后2次抛掷一枚骰子,将得到的点数分别记为a, b.
(1)求直线ax+by+5=0与圆 相切的概率;
相切的概率;
(2)将a,b,5的值分别作为三条线段的长,求这三条线段能围成等腰三角形(含等边三角形)的概率.
已知a>0,a≠1,设p:函数 内单调递减,q:曲线y=x2+(2a-3)x+1与x轴交于不同的两点.如果p与q有且只有一个正确,求a的取值范围
内单调递减,q:曲线y=x2+(2a-3)x+1与x轴交于不同的两点.如果p与q有且只有一个正确,求a的取值范围
规定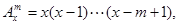 其中
其中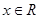 ,
,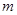 为正整数,且
为正整数,且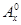 =1,这是排列数
=1,这是排列数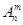 (
(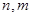 是正整数,
是正整数,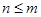 )的一种推广.
)的一种推广.
(Ⅰ) 求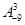 的值;
的值;
(Ⅱ)排列数的两个性质:①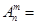
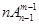 ,②
,②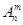
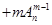
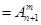 (其中m,n是正整数).是否都能推广到
(其中m,n是正整数).是否都能推广到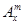 (
(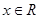 ,
,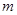 是正整数)的情形?若能推广,写出推广的形式并给予证明;若不能,则说明理由;
是正整数)的情形?若能推广,写出推广的形式并给予证明;若不能,则说明理由;
(Ⅲ)已知函数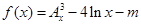 ,试讨论函数
,试讨论函数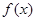 的零点个数.
的零点个数.
甲、乙两人玩猜数字游戏,规则如下:
①连续竞猜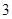 次,每次相互独立;
次,每次相互独立;
②每次竟猜时,先由甲写出一个数字,记为 ,再由乙猜测甲写的数字,记为
,再由乙猜测甲写的数字,记为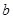 ,已知
,已知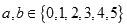 ,若
,若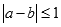 ,则本次竞猜成功;
,则本次竞猜成功;
③在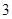 次竞猜中,至少有
次竞猜中,至少有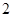 次竞猜成功,则两人获奖.
次竞猜成功,则两人获奖.
(Ⅰ) 求甲乙两人玩此游戏获奖的概率;
(Ⅱ)现从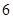 人组成的代表队中选
人组成的代表队中选 人参加此游戏,这
人参加此游戏,这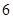 人中有且仅有
人中有且仅有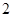 对双胞胎,记选出的
对双胞胎,记选出的 人中含有双胞胎的对数为
人中含有双胞胎的对数为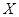 ,求
,求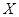 的分布列和期望.
的分布列和期望.