、(满分17分)
设数列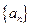 的前
的前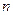 项和为
项和为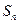 ,对任意的正整数
,对任意的正整数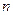 ,都有
,都有 成立,记
成立,记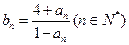 。
。
(I)求数列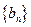 的通项公式;
的通项公式;
(II)记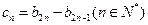 ,设数列
,设数列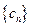 的前
的前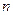 项和为
项和为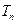 ,求证:对任意正整数
,求证:对任意正整数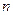 都有
都有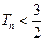 ;
;
已知在 的展开式中,第6项为常数项。
的展开式中,第6项为常数项。
(1)求 ;(2)求
;(2)求 的项的系数;(3)求展开式中所有的有理项。
的项的系数;(3)求展开式中所有的有理项。
用0,1,2,3,4,5这六个数字:
(Ⅰ)可组成多少个无重复数字的自然数?
(Ⅱ)可组成多少个无重复数字的四位偶数?
(Ⅲ)组成无重复数字的四位数中比4023大的数有多少?
(本小题满分11分)已知函数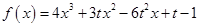 ,其中
,其中 .
.
(1) 当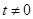 时,求
时,求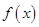 的单调区间;
的单调区间;
(2) 证明:对任意 ,
,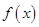 在区间
在区间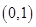 内存在零点.
内存在零点.
(本小题满分11分)对于定义域为D的函数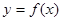 ,如果存在区间
,如果存在区间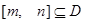 ,同时满足:
,同时满足:
①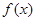 在
在 内是单调函数;
内是单调函数;
②当定义域是 时,
时,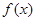 的值域也是
的值域也是 .
.
则称 是该函数的“和谐区间”.
是该函数的“和谐区间”.
(1)证明: 是函数
是函数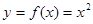 的一个“和谐区间”.
的一个“和谐区间”.
(2)求证:函数 不存在“和谐区间”.
不存在“和谐区间”.
(3)已知函数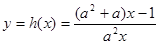 (
(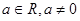 )有“和谐区间”
)有“和谐区间” ,当
,当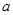 变化时,求出
变化时,求出 的最大值.
的最大值.
(本小题满分10分) 定义域为 的奇函数
的奇函数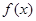 满足
满足 ,且当
,且当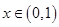 时,
时, .
.
(1)求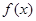 在
在 上的解析式;
上的解析式;
(2)当 取何值时,方程
取何值时,方程 在
在 上有解?
上有解?