(本小题满分11分)对于定义域为D的函数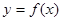
，如果存在区间
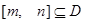，同时满足：
①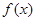
在
内是单调函数；
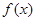②当定义域是时，的值域也是．
则称是该函数的“和谐区间”．
（1）证明：
是函数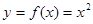
的一个“和谐区间”．
（2）求证：函数
不存在“和谐区间”．
（3）已知函数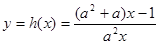
（
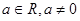）有“和谐区间”，当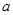
变化时，求出
的最大值．
(本题满分10分)某汽车运输公司购买了一批豪华大客车投入运营．据市场分析，每辆客车运营的总利润y(单位：十万元)与运营年数x满足二次函数的关系：
,且该二次函数图像过点(4,7)．问每辆客车运营多少年，运营的年平均利润最大？最大值为多少？(年平均利润=
)
(本题满分9分)设锐角三角形ABC的内角A，B，C的对边分别为a，b，c，
．
（1）求B的大小；
（2）若
的面积等于
，C=2,求
和
的值。
(本题满分9分) 已知数列
的前n项和为
，且
．
（1）求数列
的通项公式；(2) 当n为何值时，
达到最大？最大值是多少？
(本题满分8分)若集合
，集合
，求集合A
B．
(本题满分6分) 画出不等式组
所表示的平面区域（在所提供的平面直角坐标系内用阴影表示），并求出该平面区域的面积
