((本小题满分12分)
已知椭圆C: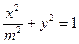 (常数
(常数 ),P是曲线C上的动点,M是曲线C的右
),P是曲线C上的动点,M是曲线C的右
顶点,定点A的坐标为(2,0).
(1)若M与A重合,求曲线C的焦点坐标.
(2)若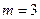 ,求|PA|的最大值与最小值.
,求|PA|的最大值与最小值.
(3)若|PA|最小值为|MA|,求实数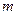 的取值范围.
的取值范围.
如果实数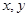 满足
满足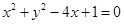 ,求①
,求①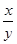 的最大值;②
的最大值;②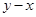 的最小值;
的最小值;
③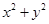 的最值.
的最值.
若曲线C: 和直线
和直线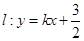 只有一个公共点,那么
只有一个公共点,那么 的值为 ()
的值为 ()
A.0或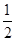 |
B.0或 |
C. 或 或 |
D.0或 或 或 |
设 为双曲线
为双曲线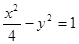 的两个焦点,点
的两个焦点,点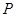 在双曲线上且满足
在双曲线上且满足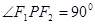 ,则
,则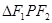 的面积是()
的面积是()
| A.1 | B.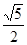 |
C.2 | D. |
若函数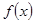 满足下列条件:在定义域内存在
满足下列条件:在定义域内存在 使得
使得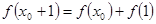 成立,则称函数
成立,则称函数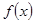 具有性质
具有性质 ;反之,若
;反之,若 不存在,则称函数
不存在,则称函数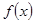 不具有性质
不具有性质 .
.
(1)证明:函数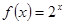 具有性质
具有性质 ,并求出对应的
,并求出对应的 的值;
的值;
(2)已知函数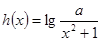 具有性质
具有性质 ,求
,求 的取值范围;
的取值范围;
(3)试探究形如① 、②
、② 、③
、③ 、④
、④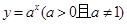 、⑤
、⑤ 的函数,指出哪些函数一定具有性质
的函数,指出哪些函数一定具有性质 ?并加以证明.
?并加以证明.
已知a>0且a≠1,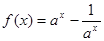 。
。
(1)判断函数f(x)是否有零点,若有求出零点;
(2)判断函数f(x)的奇偶性;
(3)讨论f(x)的单调性并用单调性定义证明。