(本小题满分14分)
如图,斜三棱柱 中,侧面
中,侧面
 底面ABC,侧面
底面ABC,侧面 是菱形,
是菱形, ,E、F分别是
,E、F分别是 、AB的中点.
、AB的中点.
求证:(1)EF∥平面 ;
;
(2)平面CEF⊥平面ABC.
(本小题满分15分)已知函数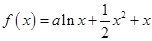 。
。
(1)求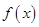 的单调区间;
的单调区间;
(2)函数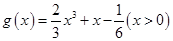 ,求证:
,求证: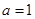 时
时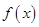 的图象都不在
的图象都不在 图象的上方.
图象的上方.
如图,三棱柱ABC—A1B1C1中,AA1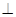 面ABC,BC
面ABC,BC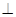 AC,BC=AC=2,D为AC的中点。
AC,BC=AC=2,D为AC的中点。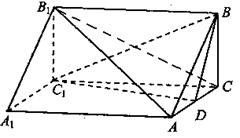
(1)若AA1=2,求证: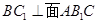 ;
;
(2)若AA1=3,求二面角C1—BD—C的余弦值.
(本小题满分14分)已知数列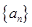 的每项均为正数,首项
的每项均为正数,首项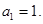 记数列
记数列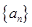 前
前 项和为
项和为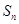 ,满足
,满足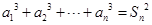 .
.
(1)求 的值及数列
的值及数列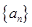 的通项公式;
的通项公式;
(2)若 ,记数列
,记数列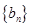 前
前 项和为
项和为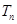 ,求证:
,求证: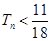 .
.
(本小题满分14分)已知向量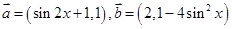 ,其中
,其中 ,函数
,函数 .
.
(1)求 的对称中心;
的对称中心;
(2)若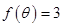 ,其中
,其中 ,求
,求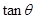 的值.
的值.
已知函数 .
.
(Ⅰ)当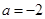 时,求函数
时,求函数 的单调区间;
的单调区间;
(Ⅱ)是否存在实数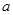 ,使得函数
,使得函数 有唯一的极值,且极值大于
有唯一的极值,且极值大于 ?若存在,,求
?若存在,,求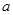 的取值
的取值
范围;若不存在,说明理由;
(Ⅲ)如果对 ,总有
,总有 ,则称
,则称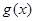 是
是 的凸
的凸
函数,如果对 ,总有
,总有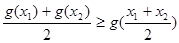 ,则称
,则称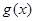 是
是 的凹函数.当
的凹函数.当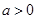 时,利用定义分析
时,利用定义分析 的凹凸性,并加以证明。
的凹凸性,并加以证明。