(本小题满分13分)为抗击金融风暴,某工贸系统决定对所属企业给予低息贷款的扶持,该系统先根据相关评分标准对各个企业进行了评估,并依据评估得分将这些企业分别评定为优秀、良好、合格、不合格4个等级,然后根据评估等级 分配相应的低息贷款金额,其评估标准和贷款金额如下表:
分配相应的低息贷款金额,其评估标准和贷款金额如下表:
| 评估得分 |
[50,60) |
[60,70) |
[70,80) |
[80,90] |
| 评定类型 |
不合格 |
合格 |
良好 |
优秀 |
| 贷款金额(万元) |
0 |
200 |
400 |
800 |
为了更好地掌控贷款总额,该系统随机抽查了所属部分企业的评估分数,得其频率分布直方图如下:
(1)估计该系统所属企业评估得分的中位数及平均分;
(2)该系统要求各企业对照评分标准进行整改,若整改后优秀企业数量不变,不合格企业、合格企业、良好企业的数量依次成等差数列,系统所属企业获得贷款的均值(即数学期望)不低于410万元,那么整改后不合格企业占企业总数的百分比的最大值是多少?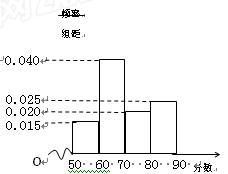
如图,在三棱柱 中,四边形
中,四边形 为菱形,
为菱形, ,四边形
,四边形 为矩形,若
为矩形,若 ,
, ,
, .
.
(1)求证: 面
面 ;
;
(2)求二面角 的余弦值;
的余弦值;
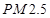 是指大气中直径小于或等于
是指大气中直径小于或等于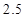 微米的颗粒物,也称为可吸入肺颗粒物.我国
微米的颗粒物,也称为可吸入肺颗粒物.我国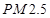 标准采用世卫组织设定的最宽限值,即
标准采用世卫组织设定的最宽限值,即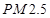 日均值在
日均值在 微克/立方米以下空气质量为一级;在
微克/立方米以下空气质量为一级;在 微克/立方米
微克/立方米 微克/立方米之间空气质量为二级;在
微克/立方米之间空气质量为二级;在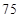 微克/立方米以上空气质量为超标.某试点城市环保局从该市市区
微克/立方米以上空气质量为超标.某试点城市环保局从该市市区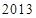 年上半年每天的
年上半年每天的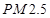 监测数据中随机的抽取
监测数据中随机的抽取 天的数据作为样本,监测值如下图茎叶图所示(十位为茎,个位为叶).
天的数据作为样本,监测值如下图茎叶图所示(十位为茎,个位为叶).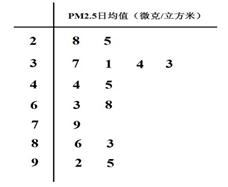
(1)在这 天的
天的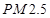 日均监测数据中,求其中位数;
日均监测数据中,求其中位数;
(2)从这 天的数据中任取
天的数据中任取 天数据,记
天数据,记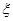 表示抽到
表示抽到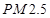 监测数据超标的天数,求
监测数据超标的天数,求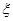 的分布列及数学期望;
的分布列及数学期望;
(3)以这 天的
天的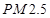 日均值来估计一年的空气质量情况,则一年(按
日均值来估计一年的空气质量情况,则一年(按 天计算)中平均有多少天的空气质量达到一级或二级.
天计算)中平均有多少天的空气质量达到一级或二级.
已知 ,
, .
.
(1)求 的值;
的值;
(2)当 时,求
时,求 的最值.
的最值.
设函数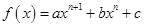
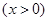 ,其中
,其中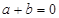 ,
, 为正整数,
为正整数,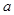 、
、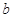 、
、 均为常数,曲线
均为常数,曲线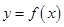 在
在 处的切线方程为
处的切线方程为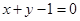 .
.
(1)求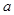 、
、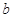 、
、 的值;
的值;
(2)求函数 的最大值;
的最大值;
(3)证明:对任意的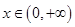 都有
都有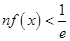 .(
.(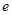 为自然对数的底)
为自然对数的底)
如图,已知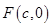 是椭圆
是椭圆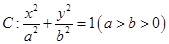 的右焦点;圆
的右焦点;圆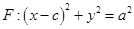 与
与 轴交于
轴交于 两点,其中
两点,其中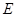 是椭圆
是椭圆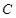 的左焦点.
的左焦点.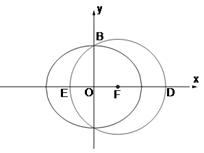
(1)求椭圆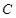 的离心率;
的离心率;
(2)设圆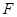 与
与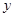 轴的正半轴的交点为
轴的正半轴的交点为 ,点
,点 是点
是点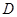 关于
关于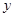 轴的对称点,试判断直线
轴的对称点,试判断直线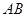 与圆
与圆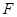 的位置关系;
的位置关系;
(3)设直线 与圆
与圆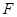 交于另一点
交于另一点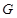 ,若
,若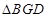 的面积为
的面积为 ,求椭圆
,求椭圆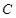 的标准方程.
的标准方程.