如图,已知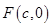 是椭圆
是椭圆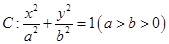 的右焦点;圆
的右焦点;圆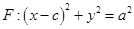 与
与 轴交于
轴交于 两点,其中
两点,其中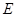 是椭圆
是椭圆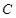 的左焦点.
的左焦点.
(1)求椭圆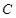 的离心率;
的离心率;
(2)设圆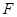 与
与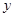 轴的正半轴的交点为
轴的正半轴的交点为 ,点
,点 是点
是点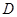 关于
关于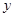 轴的对称点,试判断直线
轴的对称点,试判断直线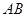 与圆
与圆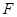 的位置关系;
的位置关系;
(3)设直线 与圆
与圆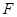 交于另一点
交于另一点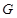 ,若
,若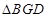 的面积为
的面积为 ,求椭圆
,求椭圆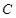 的标准方程.
的标准方程.
如图,三棱锥SABC中,SC丄底面ABC, ,
, ,M
,M 为SB中点,N在AB上,满足
为SB中点,N在AB上,满足

(I)求点N到平面SBC的距离;
(II)求二面角C-MN-B的大小.
现有三种基本电子模块 ,电流能通过
,电流能通过 的概率都是P,电流能否通过各模块相互独立.已知
的概率都是P,电流能否通过各模块相互独立.已知 中至少有一个能通过电流
中至少有一个能通过电流 的概率为0.999.现由该电子模块组装成某预警系统M(如图所示),针对系统M而言,只要有电流通过该系统就能正常工作.
的概率为0.999.现由该电子模块组装成某预警系统M(如图所示),针对系统M而言,只要有电流通过该系统就能正常工作.
(1)求P值
(II)求预警系统M正常工作的概率
在ΔACB中,已知 ,
, ,设
,设 .
.
(I)用θ表示|CA|; (II)求.
(II)求. 的单调递增区间.
的单调递增区间.
已知函数 ,
, 为正整数.
为正整数.
(Ⅰ)求 和
和 的值;
的值;
(Ⅱ)数列 的通项公式为
的通项公式为 (
( ),求数列
),求数列 的前
的前 项和
项和 ;
;
(Ⅲ) (4分)设数列 满足:
满足: ,
, ,设
,设 ,若(Ⅱ)中的
,若(Ⅱ)中的 满足:对任意不小于3的正整数n,
满足:对任意不小于3的正整数n, 恒成立,试求m的最大值.
恒成立,试求m的最大值.
已知数列{an}的前n项和为
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若 ,数列{Cn}的前项和为Tn,求证:Tn<4.
,数列{Cn}的前项和为Tn,求证:Tn<4.