现有三种基本电子模块 ,电流能通过
,电流能通过 的概率都是P,电流能否通过各模块相互独立.已知
的概率都是P,电流能否通过各模块相互独立.已知 中至少有一个能通过电流
中至少有一个能通过电流 的概率为0.999.现由该电子模块组装成某预警系统M(如图所示),针对系统M而言,只要有电流通过该系统就能正常工作.
的概率为0.999.现由该电子模块组装成某预警系统M(如图所示),针对系统M而言,只要有电流通过该系统就能正常工作.
(1)求P值
(II)求预警系统M正常工作的概率
已知函数 处取得极值2
处取得极值2
(1)求函数 的表达式;
的表达式;
(2)当 满足什么条件时,函数
满足什么条件时,函数 在区间
在区间 上单调递增?
上单调递增?
(3)若 为
为 图象上任意一点,直线与
图象上任意一点,直线与 的图象相切于点P,求直线的斜率
的图象相切于点P,求直线的斜率 的取值范围
的取值范围
已知椭圆 的左、右焦点分别为
的左、右焦点分别为 、
、 , 焦距为2,过
, 焦距为2,过 作垂直于椭圆长轴的弦长
作垂直于椭圆长轴的弦长 为3
为3
(1)求椭圆的方程;
(2)若过点 的动直线
的动直线 交椭圆于A、B两点,判断是否存在直线
交椭圆于A、B两点,判断是否存在直线 使得
使得 为钝角,若存在,求出直线
为钝角,若存在,求出直线 的斜率
的斜率 的取值范围
的取值范围
如图,△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC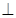 平面ABC,
平面ABC,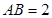 ,
,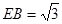
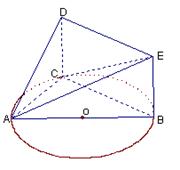
(1)证明:平面ACD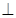 平面ADE;
平面ADE;
(2)记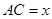 ,
,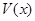 表示三棱锥A-CBE的体积,求函数
表示三棱锥A-CBE的体积,求函数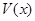 的解析式及最大值
的解析式及最大值
在数列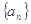 中,
中,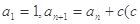 为常数,
为常数,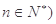 ,且
,且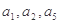 成公比不等于1的等比数列
成公比不等于1的等比数列
(1)求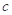 的值;
的值;
(2)设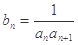 ,求数列
,求数列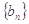 的前
的前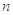 项和
项和
某中学举行了一次“环保知识竞赛”, 全校学生参加了这次竞赛.为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本进行统计.请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示)解决下列问题:
组别 |
分组 |
频数 |
频率 |
| 第1组 |
[50,60) |
8 |
0 16 |
| 第2组 |
[60,70) |
a |
▓ |
| 第3组 |
[70,80) |
20 |
0 40 |
| 第4组 |
[80,90) |
▓ |
0 08 |
| 第5组 |
[90,100] |
2 |
b |
| 合计 |
▓ |
▓ |

(1)求出 的值;
的值;
(2)在选取的样本中,从竞赛成绩是80分以上(含80分)的同学中随机抽取2名同学到广场参加环保知识的志愿宣传活动
(ⅰ)求所抽取的2名同学中至少有1名同学来自第5组的概率;
(ⅱ)求所抽取的2名同学来自同一组的概率