(本小题满分14分)
已知椭圆G与双曲线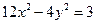 有相同的焦点,且过点
有相同的焦点,且过点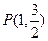 .
.
(1)求椭圆G的方程;
(2)设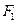 、
、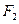 是椭圆G的左焦点和右焦点,过
是椭圆G的左焦点和右焦点,过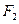 的直线
的直线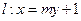 与椭圆G相交于A、B两点,请问
与椭圆G相交于A、B两点,请问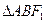 的内切圆M的面积是否存在最大值?若存在,求出这个最大值及直线
的内切圆M的面积是否存在最大值?若存在,求出这个最大值及直线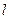 的方程,若不存在,请说明理由.
的方程,若不存在,请说明理由.
函数 (
(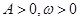 )的最大值为3, 其图像相邻两条对称轴之间的距离为
)的最大值为3, 其图像相邻两条对称轴之间的距离为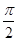 ,
,
(1)求函数 的解析式;
的解析式;
(2)设 ,则
,则 ,求
,求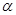 的值.
的值.
(本小题满分14分)已知 ,函数
,函数 .
.
(1)求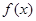 的单调区间;
的单调区间;
(2)当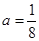 时,证明:方程
时,证明:方程 在区间(2,
在区间(2, )上有唯一解;
)上有唯一解;
(3)若存在均属于区间 的
的 且
且 ,使
,使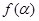 =
=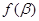 ,
,
证明: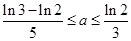 .
.
(本小题满分14分)已知等差数列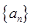 的公差为
的公差为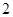 ,前
,前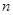 项和为
项和为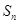 ,且
,且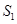 ,
, ,
,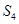 成等比数列.
成等比数列.
(1)求数列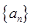 的通项公式;
的通项公式;
(2)令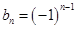
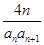 ,求数列
,求数列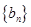 的前
的前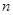 项和
项和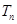 .
.
(本小题满分13分)已知椭圆 :
: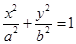
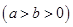 的焦距为
的焦距为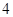 ,其短轴的两个端点与长轴的一个端点构成正三角形.
,其短轴的两个端点与长轴的一个端点构成正三角形.
(1)求椭圆 的标准方程;
的标准方程;
(2)设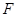 为椭圆
为椭圆 的左焦点,
的左焦点,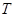 为直线
为直线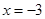 上任意一点,过
上任意一点,过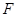 作
作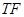 的垂线交椭圆
的垂线交椭圆 于点
于点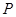 ,
,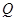 ,证明:
,证明: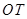 平分线段
平分线段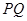 (其中
(其中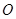 为坐标原点),
为坐标原点),
(本小题满分13分)如图甲,在平面四边形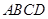 中,已知
中,已知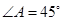 ,
,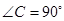 ,
,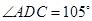 ,
,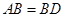 ,现将四边形
,现将四边形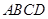 沿
沿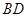 折起,使平面
折起,使平面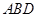
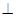 平面
平面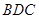 (如图乙),设点
(如图乙),设点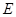 ,
,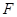 分别为棱
分别为棱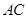 ,
,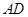 的中点.
的中点.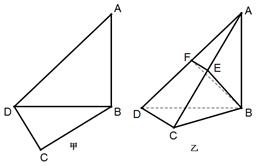
(1)证明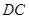
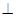 平面
平面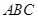 ;
;
(2)求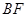 与平面
与平面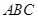 所成角的正弦值;
所成角的正弦值;
(3)求二面角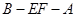 的余弦值.
的余弦值.