一种氢气燃料的汽车,质量为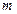 =2.0×103kg,发动机的额定输出功率为80kW,行驶在平直公路上时所受阻力恒为车重的0.1倍。若汽车从静止开始先匀加速启动,加速度的大小为
=2.0×103kg,发动机的额定输出功率为80kW,行驶在平直公路上时所受阻力恒为车重的0.1倍。若汽车从静止开始先匀加速启动,加速度的大小为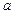 =1.0m/s2。达到额定输出功率后,汽车保持功率不变又加速行驶了800m,直到获得最大速度后才匀速行驶。g=10m/s2,试求:
=1.0m/s2。达到额定输出功率后,汽车保持功率不变又加速行驶了800m,直到获得最大速度后才匀速行驶。g=10m/s2,试求:
(1)汽车的最大行驶速度;
(2)汽车从静止到获得最大行驶速度所用的总时间。
如图所示,在同一竖直平面内,一轻质弹簧一端固定,另一自由端恰好与水平线AB平齐,静止放于倾角为60°的光滑斜面上。一长为L=10cm的轻质细绳一端固定在O点,另一端系一质量为m=1 kg的小球,将细绳拉至水平,使小球在位置C由静止释放,小球到达最低点D时,细绳刚好被拉断。之后小球在运动过程中恰好沿斜面方向将劲度系数为k=100N/m的弹簧压缩,已知弹簧的弹性势能EP与弹簧的劲度系数k及弹簧的形变量x的关系式为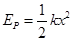 。g=10 m/s2,求:
。g=10 m/s2,求: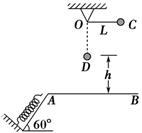
(1) 当弹簧的形变量为x=9cm时小球的加速度大小;
(2) D点到水平线AB的高度h;
(3) 在小球的运动过程中,小球的动能最大值。
如图所示,一块足够大的光滑平板放置在水平面上,能绕水平固定轴MN调节其与水平面所成的倾角。板上一根长为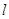 ="0." 60m的轻细绳,它的一端系住一质量为0.2kg的小球P,另一端固定在板上的O点。先将轻绳平行于水平轴MN拉直,然后给小球一沿着平板并与轻绳垂直的初速度v0=3.0m/s。重力加速度g=l0
="0." 60m的轻细绳,它的一端系住一质量为0.2kg的小球P,另一端固定在板上的O点。先将轻绳平行于水平轴MN拉直,然后给小球一沿着平板并与轻绳垂直的初速度v0=3.0m/s。重力加速度g=l0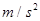
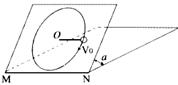
(1)求当平板的倾角固定为90º,小球经过运动轨迹的最低点时轻细绳中的拉力大小;
(2)当平板的倾角固定为α时,若小球能保持在板面内作圆周运动,倾角α的值应在什么范围内?
甲、乙两汽车沿同一平直公路同向匀速行驶,甲车在前,乙车在后,它们行驶的速度均为16 m/s。遇到情况后,甲车紧急刹车,乙车司机看到甲车刹车后也采取紧急刹车。已知甲车紧急刹车时加速度a1=3 m/s2,乙车紧急刹车时加速度a2=4 m/s2,乙车司机的反应时间是0.5 s(即乙车司机看到甲车刹车后0.5 s才开始刹车)。
(1)甲车紧急刹车后,经过多长时间甲、乙两车的速度相等?
(2)为保证两车紧急刹车过程不相碰,甲、乙两车行驶过程至少应保持多大距离?
(12分)如图所示,一半径为R的绝缘圆形轨道竖直放置,圆轨道最低点与一条水平轨道相连,轨道都是光滑的.轨道所在空间存在水平向右的匀强电场,场强为E.从水平轨道上的A点由静止释放一质量为m的带正电的小球,为使小球刚好在圆轨道内做圆周运动,求释放点A距圆轨道最低点B的距离s。已知小球受到的电场力大小等于小球重力的 倍。
倍。
(10分)如图所示,水平放置的两块平行金属板长l =5cm,两板间距d=1cm,两板间电压为U=90V,且上板带正电,一个电子沿水平方向以速度v0=2.0×107m/s,从两板中央射入,(电子质量m=9.0×10-31kg,电子电量值q=1.6×10-19C)求: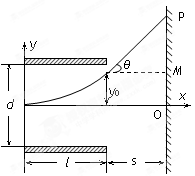
(1)电子飞出金属板时侧位移y0是多少?
(2)电子离开电场后,打在屏上的P点,若s=10cm,求OP的长.