(本小题满分13分)为抗击金融风暴，某工贸系统决定对所属企业给予低息贷款的扶持，该系统先根据相关评分标准对各个企业进行了评估，并依据评估得分将这些企业分别评定为优秀、良好、合格、不合格4个等级，然后根据评估等级
分配相应的低息贷款金额，其评估标准和贷款金额如下表：
| 评估得分 |
[50，60) |
[60，70) |
[70，80) |
[80，90] |
| 评定类型 |
不合格 |
合格 |
良好 |
优秀 |
| 贷款金额(万元) |
0 |
200 |
400 |
800 |
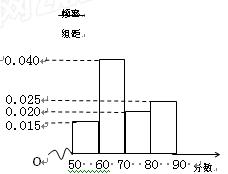
为了更好地掌控贷款总额，该系统随机抽查了所属部分企业的评估分数，得其频率分布直方图如下
(1)估计该系统所属企业评估得分的中位数及平均分；
(2)该系统要求各企业对照评分标准进行整改，若整改后优秀企业数量不变，不合格企业、合格企业、良好企业的数量依次成等差数列，系统所属企业获得贷款的均值(即数学期望)不低于410万元，那么整改后不合格企业占企业总数的百分比的最大值是多少？
在同一平面内，且
.
，且
，求
；
，且
，求
与
的夹角.
，
，点A
.
满足
,求
和
的值.
. 
的定义域及最小正周期；
ABC所在平面内一点，且满足：
.
，求
的值.