(本小题满分12分)节能减排是现代生活的追求。长沙地区某一天的温度(单位: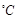 )随时间
)随时间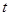 (单位:小时)的变化近似满足函数关系:
(单位:小时)的变化近似满足函数关系: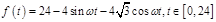 ,
,
且早上8时的温度为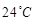 ,
, .
.
(Ⅰ)求函数的解析式,并判断这一天的最高温度是多少?出现在何时?
(Ⅱ)某通宵营业的超市,为节约能源和开支,在环境温度超过 时,才开启中央空调降温,否则关闭中央空调,问中央空调应在何时开启?何时关闭?
时,才开启中央空调降温,否则关闭中央空调,问中央空调应在何时开启?何时关闭?
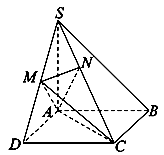
(本小题满分12分)如图,在四棱锥 中,底面
中,底面 是正方形,
是正方形,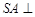 底面
底面 ,
, , 点
, 点 是
是 的中点,
的中点,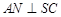 ,且交
,且交 于点
于点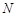 .
.
(Ⅰ)求证: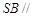 平面
平面 ;
;
(Ⅱ)求证:平面 ⊥平面
⊥平面 ;
;
(Ⅲ)求二面角 的余弦值.
的余弦值.
(本小题满分12分)某高中数学竞赛培训在某学段共开设有初等代数、平面几何、初等数论和微积分初步共四门课程,要求初等数论、平面几何都要合格,且初等代数和微积分初步至少有一门合格,则能取得参加数学竞赛复赛的资格.现有甲、乙、丙三位同学报名参加数学竞赛培训,每一位同学对这四门课程考试是否合格相互独立,其合格的概率均相同(见下表),且每一门课程是否合格相互独立.
(Ⅰ)求甲同学取得参加数学竞赛复赛的资格的概率;
(Ⅱ)记 表示三位同学中取得参加数学竞赛复赛的资格的人数,求
表示三位同学中取得参加数学竞赛复赛的资格的人数,求 的分布列及期望
的分布列及期望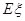 .
.
已知函数 ,
, .
.
(1)已知 在
在 上是单调函数,求
上是单调函数,求 的取值范围;
的取值范围;
(2)已知 满足
满足 ,且
,且 ,试比较
,试比较 与
与 的大小;
的大小;
(3)已知 ,是否存在正数
,是否存在正数 ,使得关于
,使得关于 的方程
的方程 在
在 上有两个不相等的实数根?如果存在,求
上有两个不相等的实数根?如果存在,求 满足的条件;如果不存在,说明理由.
满足的条件;如果不存在,说明理由.
已知椭圆C: 的离心率为
的离心率为 ,
, 是椭圆的两个焦点,
是椭圆的两个焦点, 是椭圆上任意一点,且
是椭圆上任意一点,且 的周长是
的周长是 .
.
(1)求椭圆C的方程;
(2)设圆T: ,过椭圆的上顶点作圆T的两条切线交椭圆于E、F两点,当圆心在
,过椭圆的上顶点作圆T的两条切线交椭圆于E、F两点,当圆心在 轴上移动且
轴上移动且 时,求
时,求 的斜率的取值范围.
的斜率的取值范围.