(本小题满分12分)某高中数学竞赛培训在某学段共开设有初等代数、平面几何、初等数论和微积分初步共四门课程,要求初等数论、平面几何都要合格,且初等代数和微积分初步至少有一门合格,则能取得参加数学竞赛复赛的资格.现有甲、乙、丙三位同学报名参加数学竞赛培训,每一位同学对这四门课程考试是否合格相互独立,其合格的概率均相同(见下表),且每一门课程是否合格相互独立.
(Ⅰ)求甲同学取得参加数学竞赛复赛的资格的概率;
(Ⅱ)记 表示三位同学中取得参加数学竞赛复赛的资格的人数,求
表示三位同学中取得参加数学竞赛复赛的资格的人数,求 的分布列及期望
的分布列及期望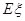 .
.
已知数列 中,
中, ,下列伪代码的功能是求数列
,下列伪代码的功能是求数列 的第
的第 项
项 的值
的值 ,现给出此算法流程图的一部分.
,现给出此算法流程图的一部分.
(1)直接写出流程图中的空格①、②处应填上的内容,并写出 与
与 之间的关系;
之间的关系;
(2)若输入的 值为2015,求输出的
值为2015,求输出的 值(写明过程).
值(写明过程).
我县某中学为了配备高一新生中寄宿生的用品,招生前随机抽取部分准高一学生调查其上学路上所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中上学路上所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].
(1)求直方图中 的值;
的值;
(2)如果上学路上所需时间不少于40分钟的学生应寄宿,且该校计划招生1800名,请估计新生中
应有多少名学生寄宿;
(3)若不安排寄宿的话,请估计所有学生上学的平均耗时(用组中值代替各组数据的平均值).
设函数 是定义域为
是定义域为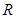 的奇函数.
的奇函数.
(1)求 值;
值;
(2)若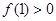 ,试判断函数单调性,并求使不等式
,试判断函数单调性,并求使不等式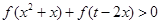 恒成立的
恒成立的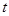 的取值范围;
的取值范围;
(3)若 ,设
,设 ,
, 在
在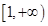 上的最小值为
上的最小值为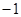 ,求
,求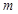 的值.
的值.
已知函数 在区间
在区间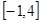 上有最大值10和最小值1.
上有最大值10和最小值1.
设 .
.
求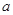 、
、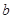 的值;
的值;
证明:函数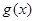 在
在 上是增函数
上是增函数
若不等式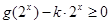 在
在 上有解,求实数
上有解,求实数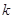 的取值范围;
的取值范围;
甲厂根据以往的生产销售经验得到下面有关生产销售的统计规律:每生产产品 (百台),其总成本为
(百台),其总成本为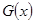 (万元),其中固定成本为2.8万元,并且每生产1百台的生产成本为1万元(总成本=固定成本+生产成本),销售收入
(万元),其中固定成本为2.8万元,并且每生产1百台的生产成本为1万元(总成本=固定成本+生产成本),销售收入 (万元)满足
(万元)满足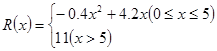 ,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
(1)写出利润函数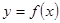 的解析式(利润=销售收入-总成本);
的解析式(利润=销售收入-总成本);
(2)要使甲厂有盈利,求产量 的范围;
的范围;
(3)甲厂生产多少台产品时,可使盈利最多?