（本小题满分10分）建华小区准备新建50个停车位，以解决小区停车难的问题.已知新建1个地上停车位和1个地下停车位需0.5万元；新建3个地上停车位和2个地下停车位需1.1万元.
（1）该小区新建1个地上停车位和1个地下停车位各需多少万元？
（2）若该小区预计投资金额超过10万元而不超过11万元，则共有几种建造方案？
（3）已知每个地上停车位月租金100元，每个地下停车位月租金30
0元. 在（2）的条件下，
新
建停车位全部租出.若该小区将第一个月租金收入中的3600元用于旧车位的维修，其余收
入继续兴建新车位，恰好用完，请直接写出该小区选择的是哪种建造方案？
小武新家装修，在装修客厅时，购进彩色地砖和单色地砖共100块，共花费5600元．已知彩色地砖的单价是80元/块，单色地砖的单价是40元/块．
（1）两种型号的地砖各采购了多少块？
（2）如果厨房也要铺设这两种型号的地砖共60块，且采购地砖的费用不超过3200元，那么彩色地砖最多能采购多少块？
如图所示的平面直角坐标系中， 将△ABC平移后得到△DEF．已知B点平移的对应点E点（0，－3）（A点与D点对应，C点与F点对应）．
（1）△ABC的面积为 ;
（2）画出平移后的△DEF，并写出点D的坐标为，点F的坐标为;
（3）若线段DF交y轴于P， 则点P的坐标为．
武汉轻轨一号线开通后学生上学大为便捷．为了了解学生上学所用的交通工具的乘坐情况，在全校学生中进行随机抽样调查，并根据收集的数据绘制了下面两幅统计图（信息尚不完整），请根据图中提供的信息，解答下面的问题：
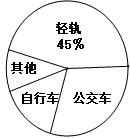
（1）此次共调查了名同学；
（2）将条形图补充完整，并计算扇形统计图中公交车部分的圆心角的度数；
（3）如果全校共有1000名学生，估计该校乘坐轻轨上学的学生有 人．
解不等式
≤
并在数轴上表示其解集．
解方程组
（1）
（2）