为保护学生视力,课桌椅的高度都是按一定的关系配套设计的,研究表明:假设课桌的高度为 cm,椅子的高度为
cm,椅子的高度为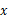 cm,则
cm,则 应是
应是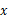 的一次函数,下表列出两套符合条件的课桌椅的高度:
的一次函数,下表列出两套符合条件的课桌椅的高度:
| |
第一套 |
第二套 |
椅子高度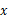 (cm) (cm) |
40 |
37 |
课桌高度 (cm) (cm) |
75 |
70 |
(1)请确定 与
与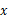 的函数关系式.
的函数关系式.
(2)现有一把高39 cm的椅子和一张高78.2 cm的课桌,它们是否配套?为什么?
问题提出:用n根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
问题探究:不妨假设能搭成 种不同的等腰三角形,为探究
种不同的等腰三角形,为探究 之间的关系,我们可以从特殊入手,通过试验、观察、类比,最后归纳、猜测得出结论.
之间的关系,我们可以从特殊入手,通过试验、观察、类比,最后归纳、猜测得出结论.
探究一:
用3根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
此时,显然能搭成一种等腰三角形。所以,当 时,
时,
用4根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
只可分成1根木棒、1根木棒和2根木棒这一种情况,不能搭成三角形
所以,当 时,
时,
用5根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
若分成1根木棒、1根木棒和3根木棒,则不能搭成三角形
若分为2根木棒、2根木棒和1根木棒,则能搭成一种等腰三角形
所以,当 时,
时,
用6根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
若分成1根木棒、1根木棒和4根木棒,则不能搭成三角形
若分为2根木棒、2根木棒和2根木棒,则能搭成一种等腰三角形
所以,当 时,
时,
综上所述,可得表①
 |
3 |
4 |
5 |
6 |
 |
1 |
0 |
1 |
1 |
探究二:
用7根相同的木棒搭成一个三角形,能搭成多少种不同的等腰三角形?
(仿照上述探究方法,写出解答过程,并把结果填在表②中)
分别用8根、9根、10根相同的木棒搭成一个三角形,能搭成多少种不同的等腰三角形?(只需把结果填在表②中)
 |
7 |
8 |
9 |
10 |
 |
你不妨分别用11根、12根、13根、14根相同的木棒继续进行探究,……
解决问题:用 根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
(设 分别等于
分别等于 、
、 、
、 、
、 ,其中
,其中 是整数,把结果填在表③中)
是整数,把结果填在表③中)
 |
 |
 |
 |
 |
 |
问题应用:用2016根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?(要求写出解答过程)
其中面积最大的等腰三角形每个腰用了__________________根木棒。(只填结果)
如图,在等边三角形ABC中,点D,E分别在边BC,AC上,DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.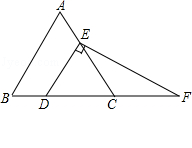
(1)求∠F的度数;
(2)若CD=2,求DF的长.
如图正方形ABCD的边长为4,E、F分别为DC、BC中点.
(1)求证:△ADE≌△ABF.
(2)求△AEF的面积.
如图,已知点A、F、E、C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE.
写出图中全等的三角形,并选择其中一对进行证明.
如图,在△ABC和△ABD中,AC与BD相交于点E,AD=BC,∠DAB=∠CBA,求证:AC=BD.