某车间有甲、乙两条生产线.在甲生产线已生产了200吨成品后,乙生产线开始投入生产,甲、乙两条生产线每天分别生产20吨和30吨成品.
(1)分别求出甲、乙两条生产线各自总产量 (吨)与从乙开始投产以来所用时间
(吨)与从乙开始投产以来所用时间 (天)之间的函数关系式.
(天)之间的函数关系式.
(2)作出上述两个函数在如图所示的直角坐标系中的图象,观察图象,分别指出第10天和第30天结束时,哪条生产线的总产量高?
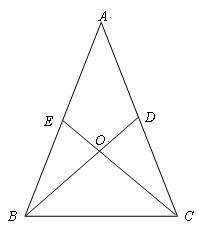
如图所示,在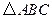 中,
中, 分别是
分别是 和
和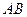 上的一点,
上的一点,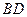 与
与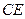 交于点
交于点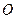 ,给出下列四个条件:①
,给出下列四个条件:①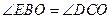 ;②
;②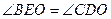 ;③
;③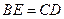 ;④
;④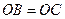 .
.
(1)上述四个条件中,哪两个条件可以判定
 是等腰三角形(用序号写出所有的情形);
是等腰三角形(用序号写出所有的情形);(2)选择(1)小题中的一种情形,证明
 是等腰三角形.
是等腰三角形.
如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC面积是28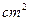 ,AB=20cm,AC=8cm,求DE的长.
,AB=20cm,AC=8cm,求DE的长.
在△ABC中,AB=CB,∠ABC=90º,F为AB延长线上一点,点E在BC上,且AE=CF.
(1)求证: Rt△ABE≌Rt△CBF;
(2)若∠CAE=30º,求∠ACF度数.
如图,一块三角形模具的阴影部分已破损.(1)如果不带残留的模具片到店铺加工一块与原来的模具△
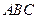 的形状和大小完全相同的模具△
的形状和大小完全相同的模具△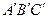 ,需要从残留的模具片中度量出哪些边、角?请简要说明理由.
,需要从残留的模具片中度量出哪些边、角?请简要说明理由.(2)作出模具
 的图形(要求:尺规作图,保留作图痕迹,不写作法和证明).
的图形(要求:尺规作图,保留作图痕迹,不写作法和证明).
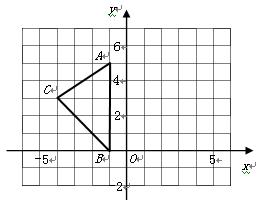
如图,在平面直角坐标系 中,
中,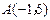 ,
,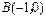 ,
,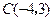 .
.(1)在图中画出
 关于
关于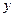 轴的对称图形
轴的对称图形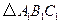 ;
;(2)直接写出点
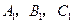 的坐标.
的坐标.