.某工厂去年某产品的年产量为100万只,每只产品的销售价为10元,固定成本为8元.今年,工厂第一次投入100万元(科技成本),并计划以后每年比上一年多投入100万元(科技成本),预计产量年递增10万只,第n次投入后,每只产品的固定成本为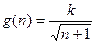 (k>0,k为常数,
(k>0,k为常数,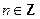 且n≥0),若产品销售价保持不变,第n次投入后的年利润为
且n≥0),若产品销售价保持不变,第n次投入后的年利润为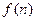 万元.
万元.
(1)求k 的值,并求出
的值,并求出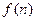 的表达式;
的表达式;
(2)问从今年算起第几年利润最高?最高利润为多少万元?
(本小题12分)
已知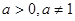 ,两个命题,
,两个命题,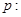 函数
函数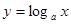 在
在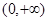 内单调递减;
内单调递减;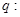 曲线
曲线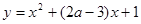 与
与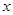 轴交于不同两点,如果
轴交于不同两点,如果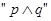 是假命题,
是假命题, 是真命题,求实数a的取值范围.
是真命题,求实数a的取值范围.
(本小题12分)已知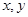 满足不等式组
满足不等式组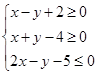 ,
,
求(1)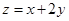 的最大值;
的最大值;
(2)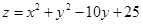 的最小值.
的最小值.
(本小题10分)已知圆心 的坐标为(1,1),圆
的坐标为(1,1),圆 与
与 轴和
轴和 轴都相切.
轴都相切.
(1)求圆 的方程;
的方程;
(2)求与圆 相切,且在
相切,且在 轴和
轴和 轴上的截距相等的直线方程.
轴上的截距相等的直线方程.
已知圆 ,圆
,圆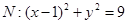 ,动圆
,动圆 与圆
与圆 外切并且与圆
外切并且与圆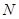 内切,圆心
内切,圆心 的轨迹为曲线
的轨迹为曲线 .
.
(1)求曲线 的轨迹方程;
的轨迹方程;
(2) 是与圆
是与圆 以及圆
以及圆 都相切的一条直线,
都相切的一条直线, 与曲线
与曲线 交于两点
交于两点 ,当圆
,当圆 的半径最长时,
的半径最长时,
求 的长.
的长.
(本小题12分)已知椭圆 的右焦点为
的右焦点为 ,点
,点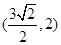 在椭圆上.
在椭圆上.
(Ⅰ)求椭圆的离心率;
(Ⅱ)点 在圆
在圆 上,且
上,且 在第一象限,过
在第一象限,过 作圆
作圆 的切线交椭圆于
的切线交椭圆于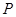 ,
, 两点,求证:△
两点,求证:△ 的周长是定值.
的周长是定值.