(本小题12分)已知椭圆 的右焦点为
的右焦点为 ,点
,点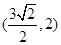 在椭圆上.
在椭圆上.
(Ⅰ)求椭圆的离心率;
(Ⅱ)点 在圆
在圆 上,且
上,且 在第一象限,过
在第一象限,过 作圆
作圆 的切线交椭圆于
的切线交椭圆于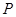 ,
, 两点,求证:△
两点,求证:△ 的周长是定值.
的周长是定值.
(本题满分12分)坛子里放着5个相同大小,相同形状的咸鸭蛋,其中有3个是绿皮的,2个是白皮的.如果不放回地依次拿出2个鸭蛋,求:
(1)第一次拿出绿皮鸭蛋的概率;
(2)第1次和第2次都拿到绿皮鸭蛋的概率;
(3)在第1次拿出绿皮鸭蛋的条件下,第2次拿出绿皮鸭蛋的概率.
( (本题满分12分)已知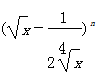 的展开式中,前三项系数的绝对值依次成等差数列.(1)求:展开式中各项系数的和;(2)求展开式中所有有理项.
的展开式中,前三项系数的绝对值依次成等差数列.(1)求:展开式中各项系数的和;(2)求展开式中所有有理项.
(本小题满分12分)在某次测验中,有6位同学的平均成绩为75分。用xn表示编号为n(n=1,2,…,6)的同学所得成绩,且前5位同学的成绩如下:
| 编号n |
1 |
2 |
3 |
4 |
5 |
| 成绩xn |
70 |
76 |
72 |
70 |
72 |
(1)求第6位同学的成绩x6,及这6位同学成绩的标准差s;
(2)从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间(68,75)中的概率。
(本小题满分12分).已知直线l:y=x+m,m∈R。若以点M(2,0)为圆心的圆与直线l相切与点P,且点P在y轴上,求该圆的方程;
(本小题满分12分)
设数列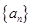 的前
的前 项和为
项和为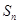 ,且方程
,且方程 有一根为
有一根为
(I)求 (II)求
(II)求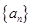 的通项公式
的通项公式