(本小题满分9分)如图12,四边形ABCD是正方形,点E,K分别在BC,AB
上,点G在BA的延长线上,且CE=BK=AG.
⑴求证:①DE=DG;②DE⊥DG;
⑵尺规作图:以线段DE,DG为边作出正方形DEFG(要求:只保留作图痕迹,不写作法和证明);
⑶连接⑵中的KF,猜想并写出四边形CEFK是怎样的特殊四边形,并证明你的猜想;
⑷当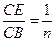 时,请直接写出
时,请直接写出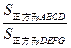 的值.
的值.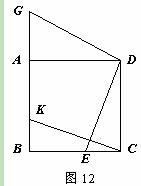
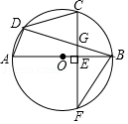
如图, 是 的直径,点 为 的中点, 为 的弦,且 ,垂足为 ,连接 交 于点 ,连接 , , .
(1)求证: ;
(2)若 ,求 的长.
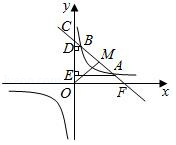
如图,一次函数 的图象与反比例函数 且 的图象在第一象限交于点 、 ,且该一次函数的图象与 轴正半轴交于点 ,过 、 分别作 轴的垂线,垂足分别为 、 .已知 , .
(1)求 的值和反比例函数的解析式;
(2)若点 为一次函数图象上的动点,求 长度的最小值.
辰星旅游度假村有甲种风格客房15间,乙种风格客房20间.按现有定价:若全部入住,一天营业额为8500元;若甲、乙两种风格客房均有10间入住,一天营业额为5000元.
(1)求甲、乙两种客房每间现有定价分别是多少元?
(2)度假村以乙种风格客房为例,市场情况调研发现:若每个房间每天按现有定价,房间会全部住满;当每个房间每天的定价每增加20元时,就会有两个房间空闲.如果游客居住房间,度假村需对每个房间每天支出80元的各种费用.当每间房间定价为多少元时,乙种风格客房每天的利润 最大,最大利润是多少元?
胜利中学为丰富同学们的校园生活,举行“校园电视台主待人“选拔赛,现将36名参赛选手的成绩(单位:分)统计并绘制成频数分布直方图和扇形统计图,部分信息如下:
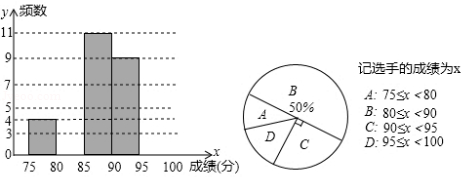
请根据统计图的信息,解答下列问题:
(1)补全频数分布直方图,并求扇形统计图中扇形 对应的圆心角度数;
(2)成绩在 区域的选手,男生比女生多一人,从中随机抽取两人临时担任该校艺术节的主持人,求恰好选中一名男生和一名女生的概率.
(1)计算: ;
(2)先化简,再求值: ,其中 , .