(本小题满分12分)如图15，在平面直角坐标系中，点P从原点O出发，沿x轴
向右以每秒1个单位长的速度运动t（t＞0）秒，抛物线y=x2＋bx＋c经过点O和点P.已知
矩形ABCD的三个顶点为A（1，0）、B（1，－5）、D（4，0）.
⑴求c、b（用含t的代数式表示）；
⑵当4＜t＜5时，设抛物线分别与线段AB、CD交于点M、N.
①在点P的运动过程中，你认为∠AMP的大小是否会变化？若变化，说明理由；若不变，求出∠AMP的值；
②求△MPN的面积S与t的函数关系式，并求t为何值时，S=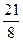
；
③在矩形ABCD的内部（不含边界），把横、纵坐标都是整数的点称为“好点”.若抛物线将这些“好点”分成数量相等的两部分，请直接写出t的取值范围.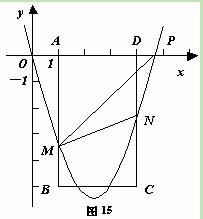
在阳光体育活动时间，小亮、小莹、小芳和大刚到学校乒乓球室打乒乓球，当时只有一副空球桌，他们只能选两人打第一场．
（1）如果确定小亮打第一场，再从其余三人中随机选取一人打第一场，求恰好选中大刚的概率；
（2）如果确定小亮做裁判，用“手心、手背”的方法决定其余三人哪两人打第一场．游戏规则是：三人同时伸“手心、手背”中的一种手势，如果恰好有两人伸出的手势相同，那么这两人上场，否则重新开始，这三人伸出“手心”或“手背”都是随机的，请用画树状图的方法求小莹和小芳打第一场的概率．
已知关于x的方程x2+2（k-3）x+k2=0有两个实数根x1、x2．
（1）求k的取值范围；
（2）若|x1+x2-9|=x1x2，求k的值．
如图，已知反比例函数y=
的图象与一次函数y=ax+b的图象相交于点A（1，4）和点B（n，-2）．
（1）求反比例函数和一次函数的解析式；
（2）当一次函数的值小于反比例函数的值时，直接写出x的取值范围．
（1）计算：2cos45°-（π+1）0+
+
（2）解方程：x（2x-5）=4x-10．
我校需刻录一批电脑光盘，若到电脑公司刻录，每张需要4元（包括空白光盘费）；若学校自刻，除买刻录机60元外，每张还需成本2元（包括空白光盘费），问刻录这批电脑光盘，到电脑公司刻录费用省，还是自刻费用省？请说明理由．