在阳光体育活动时间,小亮、小莹、小芳和大刚到学校乒乓球室打乒乓球,当时只有一副空球桌,他们只能选两人打第一场.
(1)如果确定小亮打第一场,再从其余三人中随机选取一人打第一场,求恰好选中大刚的概率;
(2)如果确定小亮做裁判,用“手心、手背”的方法决定其余三人哪两人打第一场.游戏规则是:三人同时伸“手心、手背”中的一种手势,如果恰好有两人伸出的手势相同,那么这两人上场,否则重新开始,这三人伸出“手心”或“手背”都是随机的,请用画树状图的方法求小莹和小芳打第一场的概率.
如图所示,在直角梯形ABCD中,AD=7,AB=2,DC=3,P为AD上一点,以P,A,B为顶点的三角形与以P,D,C为顶点的三角形相似,那么这样的点P有几个?为什么?
如图,D是△ABC的边AC上的一点,连接BD.已知∠ABD=∠C,AB=5,AD=4,求线段CD的长.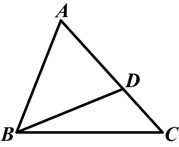
如图所示,在△ABC中,D是AC上的一点.若AB=6,AC=9,AD=4,判断△ABD与△ACB是否相似.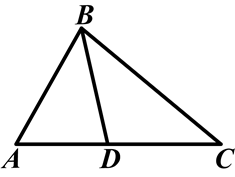
已知△ABC与△A′B′C′均为直角三角形,且∠C=∠C′=90°,AB=10cm,BC=6cm,A′B′=5cm,B′C′=3cm,那么△ABC∽△A′B′C′吗?
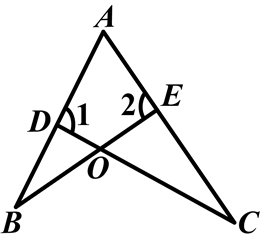
如图,若∠1=∠2,则图中有哪些三角形相似?分别把它们写出来,并说明理由.