已知:在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.
(1)直线BF垂直于直线CE于点F,交CD于点G(如图1),求证:AE=CG;
(2)直线AH垂直于直线CE,垂足为点H,交CD的延长线于点M(如图2),找出图中与BE相等的线段,并证明.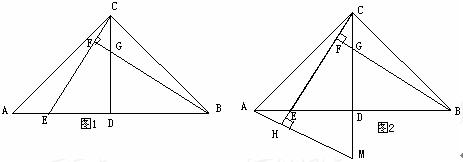
计算:
解方程:
已知:正方形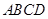 的边长为1,射线
的边长为1,射线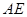 与射线
与射线 交于点
交于点 ,射线
,射线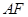 与射线
与射线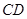 交于点
交于点 ,
, .
.
(1)如图1,当点 在线段
在线段 上时,试猜想线段
上时,试猜想线段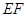 、
、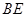 、
、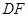 有怎样的数量关系?并证明你的猜想.
有怎样的数量关系?并证明你的猜想.
(2)设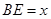 ,
,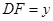 ,当点
,当点 在线段
在线段 上运动时(不包括点
上运动时(不包括点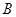 、
、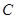 ),如图1,求
),如图1,求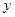 关于
关于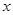 的函数解析式,并指出
的函数解析式,并指出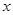 的取值范围.
的取值范围.
(3)当点 在射线
在射线 上运动时(不含端点
上运动时(不含端点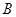 ),点
),点 在射线
在射线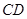 上运动.试判断以
上运动.试判断以 为圆心以
为圆心以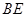 为半径的
为半径的 和以
和以 为圆心以
为圆心以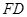 为半径的
为半径的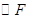 之间的位置关系.
之间的位置关系.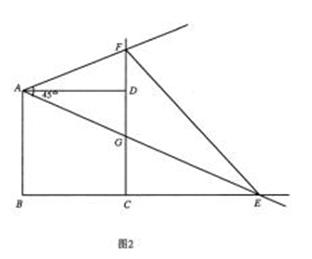
(4)当点 在
在 延长线上时,设
延长线上时,设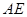 与
与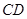 交于点
交于点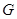 ,如图2.问△
,如图2.问△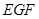 与△
与△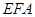 能否相似,若能相似,求出
能否相似,若能相似,求出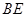 的值,若不可能相似,请说明理由.
的值,若不可能相似,请说明理由.
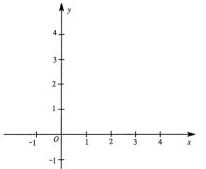
在平面直角坐标系中,已知抛物线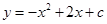 过点
过点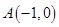 ;直线
;直线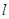 :
: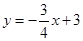 与
与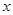 轴交于点
轴交于点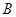 ,与
,与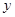 轴交于点
轴交于点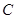 ,与抛物线的对称轴交于点
,与抛物线的对称轴交于点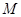 ;抛物线的顶点为
;抛物线的顶点为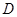 .
.
(1)求抛物线的解析式及顶点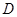 的坐标;
的坐标;
(2)过点 作
作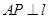 于点
于点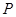 ,
,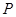 为垂足,求点
为垂足,求点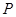 的坐标.
的坐标.
(3)若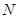 为直线
为直线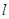 上一动点,过点
上一动点,过点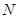 作
作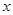 轴的垂线与抛物线交于点
轴的垂线与抛物线交于点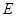 .问:是否存在这样的点
.问:是否存在这样的点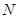 ,使得点
,使得点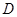 、
、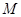 、
、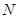 、
、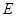 为顶点的四边形为平行四边形?若存在,求出点
为顶点的四边形为平行四边形?若存在,求出点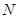 的横坐标;若不存在,请说明理由.
的横坐标;若不存在,请说明理由.
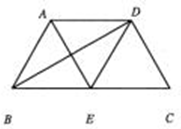
如图,在梯形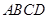 中,
中,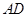 ∥
∥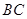 ,
,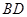 平分
平分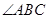 ,
,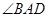 平分线交
平分线交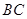 于
于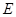 ,联结
,联结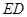 .
.
(1)求证:四边形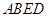 是菱形;
是菱形;
(2)当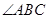 =60°,
=60°,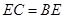 时,证明:梯形
时,证明:梯形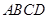 是等腰梯形.
是等腰梯形.